Pues la pregunta de cómo queda finalmente la gráfica de tensiones al formarse la rótula la vamos a contestar pero le daré un enfoque personal para que se entienda de manera más sencilla.
Toda la explicación sobre una viga cargada y los esfuerzos en la sección transversal debemos verlo como una idealización que tiene la intención de explicar los fenómenos. En realidad esta idealización de una distribución de tensiones de forma triangular es sólo eso: Una manera simple de explicar, pero no es triangular en la realidad, al menos en el concreto. Podríamos decir que debiera asemejarse.
Pues, en su estado original (Reposo) la viga está horizontal y las infinitas secciones transversales están en posición vertical, ortogonal al su eje longitudinal. Imaginemos una viga de un tramo simplemente apoyada y con carga uniforme creciente y distribuida.
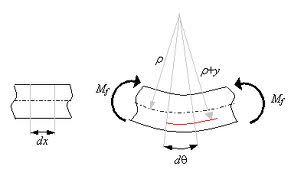
A medida que aplicamos carga a esa viga su eje longitudinal se va curveando, siendo el ángulo de curvatura mayor en los apoyos que en el centro. Asimismo las secciones transversales que antes eran verticales y ortogonales al eje longitudinal, tratan de mantenerse ortogonales pero se van inclinando y su inclinación se hace máxima en la cercanía a los apoyos donde el ángulo de curvatura es máximo. Si tenemos curveada la viga y tomamos una espada y rebanamos por secciones, digamos cada centímetro, tendremos secciones más cercanas a lo vertical en el centro o donde esté ubicado el momento flexor máximo y más inclinadas acercándose estas secciones o caras al eje horizontal en los apoyos.
Por otro lado la presión hacia debajo de las cargas que curvan la viga crea, como ya sabemos, compresión en las fibras superiores y tracción en las inferiores. Pero por qué?: Esto se debe a que al curvarse por las cargas la viga, a la vez, tiende a alargarse hacia afuera de los apoyos, pero estos crean una reacción contraria que se refleja en la sección transversal de manera que esa reacción comprime la sección es la y tracciona abajo. Esa es la explicación para los que no entienden como una reacción vertical puede generar tensiones cuasi horizontales en la sección transversal.
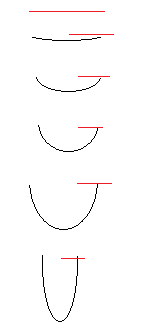
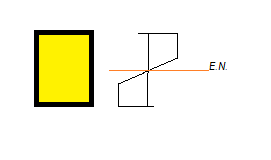
Cuando el punto más extremo de la sección llega a la Tensión de Fluencia fy los puntos más cercanos del extremo hacia el eje neutro van tomando ese valor hasta acercarse al E.N. En realidad en el E.N. nunca llegará a ser fy, sino cero, pero por idealización se asume que el gráfico es cuadrangular. En la realidad es un trapecio.
Para que fuera un cuadrado tendría que provocarse una curvatura infinita y por ende una deformación infinita y eso es imposible sin que el material falle antes. Lo que si ocurre es que hay una degradación de la rigidez axial y a flexión en la zona plastificada.



Comments (2)
José Álvarez - 30 octubre, 2011
Le felicito Ing. José Cabrera por sus post, me gustan mucho.
Una vez un profesor de mi facultad explicó muy bien el concepto de zonas traccionadas y comprimidas con una simple goma de borrar (algo más larga de lo normal) pero que se veía insitu la deformación provocada por uno de sus dedos de la mano derecha aplicado fuerza en el medio de la goma mientras esta estaba apoyada en dos dedos de su mano izquierda, y como empezaba a resquebrajarse por la tracción en su parte inferior. También de la misma forma explicaba por que se tiene que poner las armaduras principales en la parte superior de voladizos, balcones.. con esa misma goma cogiéndola por un extremo y aplicando fuerza por el otro extremo de la goma, doblándose esta. Son formas simples pero que transmitían muy bien el concepto
Si algún día hace ese libro de, dinámica de estructuras para dummies me encantaría comprarselo
Ing. José Cabrera - 30 octubre, 2011
Gracias, sus comentarios son un estimulo y un compromiso para seguir adelante..