6 funciones de MATLAB mas utilizadas para elementos de armadura plana (Ejercicio Resuelto)

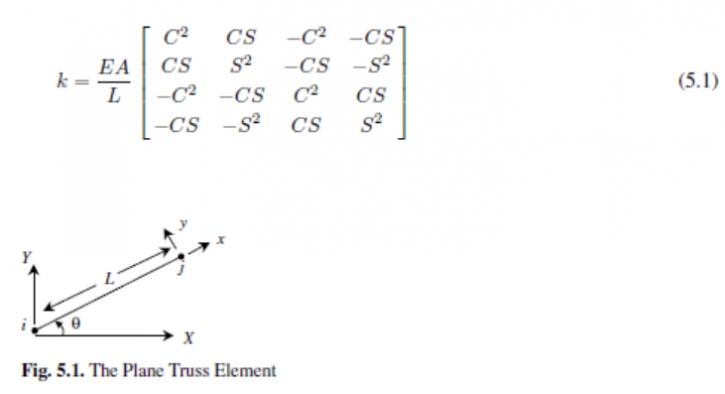
El elemento de armadura plana es un elemento finito bidimensional con tanto local como global coordenadas . Se caracteriza por funciones de forma lineales. El elemento de armazón plano tiene módulo de elasticidad E, área transversal A, y la longitud L. Cada elemento plano de cercha tiene dos nodos y está inclinada con un ángulo θ medido en sentido antihorario desde la eje X positivo global como se muestra en la Fig . 5.1 . Sea C = cos θ y S = sen θ . En este caso la matriz de elemento de rigidez está dada por (ver [ 1 ] )

1. PlaneTrussElementLength (x1, y1, x2, y2)

– Esta función devuelve la longitud del elemento dadas las coordenadas del primer nodo (x1, y1) y las coordenadas del segundo nodo (x2, y2).

2. PlaneTrussElementStiffness (E, A, L, theta)

– Esta función calcula la matriz de rigidez elemento para cada elemento de armazón plano con módulo de elasticidad E, área transversal A, longitud L, y ángulo theta (en grados). Devuelve el 4 × 4 matriz de rigidez elemento k.

3. PlaneTrussAssemble (K, k, i, j)

– Esta función ensambla la matriz k elemento de rigidez del elemento de armazón plano que une los nodos i y j en la matriz de rigidez global K. Se devuelve el 2n × 2n matriz de rigidez global K cada vez que un elemento se ensambla.

4. PlaneTrussElementForce (E, A, L, theta, u)

– Esta función calcula la fuerza de elemento utilizando el módulo de elasticidad E, el área de sección transversal A, la longitud L, el ángulo theta (en grados), y el desplazamiento elemento del vector u. Devuelve la fuerza en el elemento como un escalar.

5. PlaneTrussElementStress (E, L, theta, u)

– Esta función calcula la tensión elemento utilizando el módulo de elasticidad E, la longitud L, el ángulo theta (en grados), y el vector de elemento de desplazamiento u. Se devuelve la tencion del elemento como un escalar.

6. PlaneTrussInclinedSupport (T, i, alfa)

– Esta función calcula la matriz de transformación del soporte inclinado utilizando el número de nodo i del soporte inclinado y el ángulo de inclinación alfa (en grados). Se devuelve el 2n × 2n matriz de transformación.

DESCARGAR EJERCICIO AQUÍ