Este artículo está hecho para aquellas personas que no hayan cursado la asignatura “Dinámica Estructural” o “Mecánica de Vibraciones” o que al tratar de leer un texto de esas disciplinas no logre entenderlo.
Cuando queremos explicar científicamente el movimiento o desplazamiento de una edificación usamos un modelo Físico-Matemático considerado como el más simple existente:
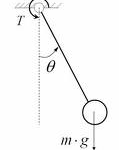
-Un Péndulo.
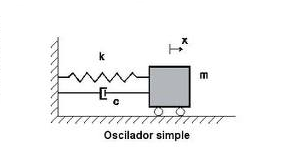
-Un resorte conectado a una masa.
Tanto el péndulo como el resorte están conectados a una masa. El resorte representa la posibilidad de desplazamiento en una dirección y la masa representa a la correspondiente a un entrepiso de una edificación. Se supone que tanto el desplazamiento como la masa se verificaran en el lugar de la losa de entrepiso que es lo que llamamos como Diafragma Rígido.
Sabemos por la física que F = k.x esto nos dice que una fuerza es igual a la constante elástica del resorte multiplicado por el desplazamiento. Como es posible que el péndulo o el resorte tengan diferentes trayectorias damos por válido, que la fuerza es variable en el tiempo dado que k, es constante. Si lo extrapolamos a la edificación la constante de resorte será la del entrepiso que es lo mismo que la oposición al desplazamiento del entrepiso. Podemos plantear:
M.a + K.x = 0 (1)
Esta es la Segunda Ley de Newton expresada en términos de equilibrio. Como queremos saber el cambio de los desplazamientos, velocidades o aceleraciones, que es lo que denominamos como “Respuesta en , el tiempo para una excitación dada” debemos convertir esta ecuación a una que este expresada en función del tiempo.
Recordemos que a = d2x/dt2 –> M.d2x/dt2 + K.x =0 (2)
Esta es una ecuación diferencial de segundo orden y su solución es una de las siguientes (da igual) :
x = Acos(wt) (3)
x = Asin(wt) (4)
Debemos resolver esta ecuación para poder conocer la Respuesta de la estructura, pero eso lo continuaremos en la próxima.
Si tomamos la primera y derivamos:
dx/dt =- Awsin(wt) (5)
d2x/dt2 = -Aw²cos(wt) (6)
Insertando (6) en la ecuación (2) –> K.x – Aw²cos(wt).M = 0
Dividiendo por M –> (K/M).x – Aw²cos(wt) = 0
Insertando (3) –> (K/M).Acos(wt) – Aw²cos(wt) = 0 –> Acos(wt)(K/M-w²) = 0
Como Acos(wt) multiplica a la otra parte podemos decir K/M-w² = 0 pasando Acos(wt) a multiplicar por 0 –> w² = K/M
w = Raiz (K/M) Esta es la frecuencia natural del sistema.
Esta ecuacion es la ecuacion de un sistema no amortiguado con un grado de libertad. Eso significa una estructura que solo se desplaza en una direccion (grado de libertad dinamica).
Si tenemos un portico como el siguiente:
x representa el único grado de libertad dinámica. K seria las de las columnas (12EI/L³) y vigas si se desean incluir. Las columnas suman sus rigideces porque están en paralelo.
Más adelante continuaremos estas sencillas clases.



Comments (13)
Yuri Villavicencio-Fdez - 19 agosto, 2011
La vez pasada estaba viendo una simulación creo que era del Caltech, sobre el efecto de la longitud de onda en la resonancia o amplificación como llama usted relacionándola con la altura de los edificios.
Explíqueme algo que cdro que puede resultar aclaratorio ,noto que el diagrama de la deformada del pórtico desprecia el efecto del peso propio de la estructura ¿Esto a qué se debe?¿También se desprecia el ángulo de rotación que podría generar un desplazamiento en «Y»?¿Es parte de la idealización del modelo?
Rafael Zaga - 21 agosto, 2011
Este libro te puede ayudar con tus dudad:
http://www.4shared.com/file/128888149/b7b10b9d/Dinamica_Estructural-Teoria_y_Calculo-Mario_Paz.html?s=1
Yuri Villavicencio-Fdez - 19 agosto, 2011
Muchas gracias de antemano, Ingeniero
Jose Rafael Cabrera Sepulveda - 19 agosto, 2011
Con mucho gusto. Lo que pasa es que aun no he metido el tema de la superposicion. Vamos analizando el sistema mas simple IGDL, que significa un grado de Libertad (Dinamica), o un desplazamiento posible y cuando queremos varios deplazamientos usamos la superposicion basandonos en varias tesis. Una de ellas es que hay proporcionalidad porque estamos en el rango elastico. Si estuvieramos en el inelastico tendriamos que valernos de ciertos artificios aproximativos o metodos numericos. Lo que no se toma en cuenta en el diseno sismico son las cargas no ancladas a la estructura. La «Masa» es el peso propio y ese si se considera + los elementos anclados.
Yuri Villavicencio-Fdez - 19 agosto, 2011
Ya comprendo. Esperaremos impacientes la continuación de este excelente artículo.
Jose Rafael Cabrera Sepulveda - 19 agosto, 2011
Creo que tome la idea de lo del peso propio y la deformada. Lo que pasa en dibujo supuse una gran rigidez en la viga por lo que no rota. Tambien se puede considerar la rotacion pero es mas complicado y no siempre es practico ya que no es tan grande la diferencia en algunos casos.
CivilGeek - 19 agosto, 2011
Excelente demostración… mi duda es hasta cuando podemos considerar a la losa como diafragma rígido en una edificación.
Rafael Zaga - 21 agosto, 2011
Lee el Capitulo 21 del ACI318S-05/318SR-486-05 Diafragmas estructurales o
la norma de diseño sismorresistente y de concreto armado del RNE.
Ing. José Cabrera - 20 agosto, 2011
El diafragma rigido y el flexible tienen sus parametros para definirlos. Mas adelante haremos un articulo sobre esto.
Jose Rafael Cabrera Sepulveda - 21 agosto, 2011
El ACI no es muy explicito en lo concerniente a Diafragmas. Voy a prepara un articulo sobre el tema que lo publicare entre hoy y manana.
Yuri Villavicencio-Fdez - 21 agosto, 2011
@Rafael Zaga: Gracias por el Libro
Rafael Zaga - 21 agosto, 2011
De nada, felicitaciones por tocar estos temas al Ing Jose cabrera. Exitos a todos.
PEDRO - 8 diciembre, 2011
GRACIAS PROFESOR POR TRATAR ESTE TEMA..COMO SE PUEDE ACCEDER A LA CONTINUACION Y SI FUERA TAN AMABLE ESCRIBIR ALGO SOBRE EL COMPORTAMIENTO SISMICO DE TANQUES DE AGUA SOBRE TORRES DE HORMIGON Y/O METALICAS. GRACIAS