CONCEPTOS FUNDAMENTALES PARA DEFINIR LA MATRIZ DE RIGIDEZ DE UNA ESTRUCTURA..I

Sé que muchas personas del Blog dominan esta técnica. Pero también sé que es un dolor de cabeza para otras. Mi aporte en estos artículos es hacer lo más sencillo y fácil su comprensión desde el origen hasta su determinación.

Primero debemos plantear que estaremos realizando planteamientos dentro del rango elástico y que estaremos trabajando con pequeñas deformaciones. Esto implica que podemos hacer uso de la geometría no deformada del objeto en consideración.

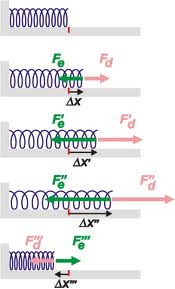
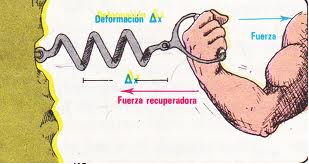
Aplicando la ley de Hooke, F=k.x

Esta ecuación se puede interpretar como que una fuerza es igual a una constante por el desplazamiento que se genera al aplicar dicha fuerza.

De manera similar podríamos decir que el desplazamiento es mayor en la medida que aumenta la fuerza, (recuerden que estamos en el rango elástico donde se cumple la proporcionalidad entre fuerza y deformación).

Ahora bien, que significa esa constante llamada constante elástica o constante de resorte?

k = F/x

Si analizamos esta formula nos dice que k es el cociente de una fuerza por un desplazamiento lo cual se puede interpretar como la fuerza que se opone a que ocurra un determinado desplazamiento.

Si halamos una tira elástica (rubber band) se deformara mucho pero sentiremos en nuestras manos una fuerza que se opone a que halemos la tira.

Si halamos un resorte sentiremos lo similar. Si lo hacemos con un amortiguador de puerta  la fuerza podría ser mayor. Si es una piedra, todavía mayor.

Porque se usa un resorte en esta idealización?: Porque es el mecanismo más simple conocido para estos fines.

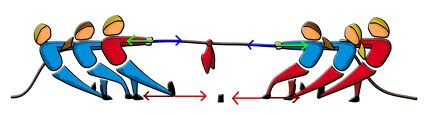
Podemos aplicar aquí que a una acción se opone una reacción. En este caso estamos hablando de fuerzas y desplazamientos, pero podríamos estar hablando de momento y rotación, aceleración,etc.

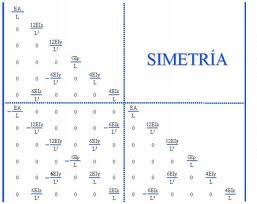
Hasta ahora hemos planteado la ecuación de una manera simple. Si tuviéramos un sistema de ecuaciones lineales simultáneas tendríamos  varias ecuaciones y diferentes incógnitas:

{F} = [K].{X}  Planteamiento matricial.

Esta es la manera de solucionar las ecuaciones desde el punto de vista matricial.

 {F} es el vector de Fuerzas. Vector, porque solo posee una columna y cada componente tiene una direccion.

{X} es el vector de Desplazamiento.

[K] es la matriz de rigidez. N  filas por n columnas, matriz cuadrada. Esta matriz estará compuesta por n x n = n² componentes y cada uno es una forma de oposición al desplazamiento.

Esta matriz estará compuesta por n² términos de acción y reacción y eso lo explicaremos con profundidad en la próxima entrega.