El problema
El problema de la viga de Michell se puede abordar desde dos puntos de vista; de manera discreta o continua.
En el primer punto de vista se ve como una estructura discreta en donde existen nodos y barras que se van agregando o quitando según la metodología.
Martinez et al. 2007 en su método de crecimiento
Antecedentes
En el caso de una optimización continua tenemos el sistema estructural como un solo elemento al que se le cambia su geometría. Esta optimización realmente es prácticamente imposible de realizar en estructuras complejas y se adopta una discretización conforme al nivel de exactitud que se requiere y también depende del procedimiento de análisis; se acostumbra usar el método del elemento finito (MEF). El discretizar se refiere a formar un mallado sobre el dominio geométrico del cuerpo a analizar.
La metodología de solución
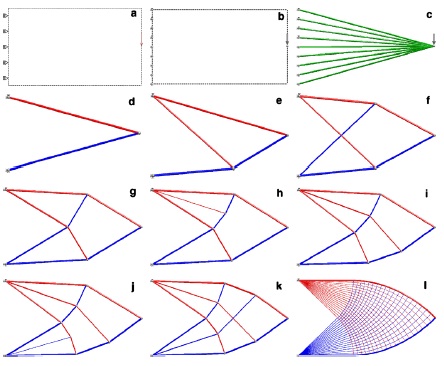
Con lo anterior definido ya nos podemos orientar en el tipo de solución que se presento en el post anterior:
Y para llegar a esta solución se puede hacer lo siguiente:
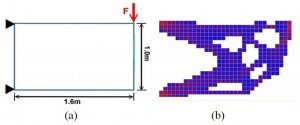
- Considerar que partimos de una pieza completa en el dominio dado, un rectángulo metálico de 1.6×1.0m
- Hacer un mallado para la pieza, la separación entre lineas de la retícula define la exactitud de la optimización a realizar.
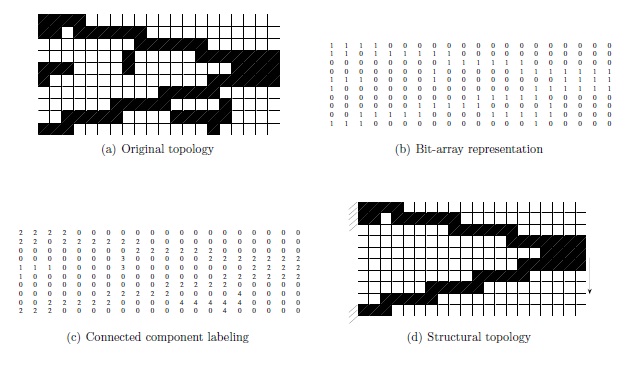
- A cada cuadricula en la malla se le asigna una posición a manera de una matriz compuesta solo de unos, esto por que inicialmente la placa esta intacta.
- Entonces se puede programar un algoritmo que quite 1’s y los sustituya por ceros (lo que representa que ya no hay material) y esto se hace de forma gradual de tal manera que no se afecte la integridad mecánica del sistema.
- Detenerse cuando todos los cambios que se propongan por más pequeños que estos sean hagan que el sistema falle bajo la carga.
Este pequeño de resumen de algoritmo realmente fue propuesto por Querin et al. en 1998 y aunque resulte demasiado evidente su concepción, no lo era para ese tiempo. Es un método muy estable pero no es muy robusto y tiene un costo computacional muy alto por que requiere analizar, prácticamente, todo el universo de soluciones. Curiosamente el algoritmo se llama «Evolutionary Structural Optimization Method» aunque no tiene que ver con la computación evolutiva.
Si a alguien le interesa el articulo se los puedo mandar.
Continuariamos con: Como la computación evolutiva resuelve la viga de Michell…


Comments (2)
Claudio pierdominici - 20 octubre, 2011
Interesante artículo, esto de probar todas las soluciones posibles lo conocia como metodos de fuerza bruta, y se podria aplicar casi a cualquier tema, pero seguimos teniendo el limitante d elas computadoras de poca capacidad… El tema de la estructura optima es uno de mis intereses desde la universidad donde un profesor nos presento un par de teoremas a modo de ejemplo, pero nunca profundizamos, creo que tampoco habria mucho material entonces..
Nayar - 20 octubre, 2011
Tienes razón Claudio en el que los métodos que analizan todas o casi todas las opciones se les llama de fuerza bruta pero hay muchas variantes de métodos de fuerza bruta, en este caso el presentado aquí es una de ellas.
Saludos y gracias por el comentario.