El Estado del Arte de la Ingeniería Sismo resistente se ha enriquecido sobremanera de la observación de las Patologías estudiadas posteriormente a los eventos sísmicos, especialmente en los últimos anos. Se ha logrado entender que muchas tradiciones en el uso de ciertas “practicas” en zonas donde no existe amenaza sísmica no pueden ser trasladadas a zonas con riesgo sísmico. Esto así porque en las zonas sin riesgo sísmico la estructura trabajara por gravedad con fuerzas verticales mientras que en las zonas de riesgo sísmico la estructura debe estar preparada para poder deformarse lateralmente (y verticalmente) debido a las oscilaciones de la excitación sísmica.
Lo anterior le confiere una importancia vital a la capacidad de deformación lateral a las edificaciones en zonas sísmicas.
Si recuerdan los artículos escritos los días 19 y 23 de Agosto: Idealización desde el punto…. y Oscilaciones Armónicas, teoría e historia, verán que toda estructura sometida a una oscilación tiene un periodo T de oscilación, una frecuencia de oscilación (inversa al periodo, f=1/T) así como K, su rigidez, que también llamamos constante de resorte.
K representa la capacidad del sistema de oponerse al movimiento o deformación. Sabemos que para una columna dependiendo de las condiciones de apoyo Ki = nE.I/L³.
Ya con esta pequeña introducción introduciremos el tema a tratar que será el de Columna Corta:
Podemos llamar Columna Corta a aquella que por su tamaño relativo a las demás del sistema al que pertenece o relativo a su diseño, en el cual fue diseñada con una longitud, pero ya construida trabajara como más corta, por lo cual tendrá mayor rigidez relativa que la que fue diseñada, podrá demandar mayores fuerzas, pero sin poder responder satisfactoriamente, por no haber sido diseñadas para esas demandas (Definición JRC).
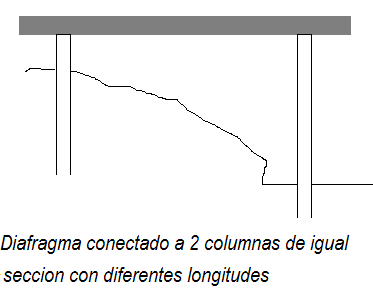
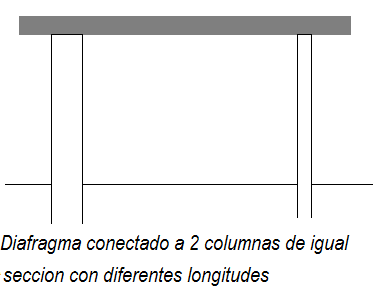
En el primer caso de la definición veamos dos columnas de diferentes longitudes unidas al mismo Diafragma. Este último al moverse aplicara el mismo desplazamiento a las dos columnas, pero, la de menor longitud tiene mayor rigidez y se opone más al movimiento que la mas, pero en su diseño no se tomó en cuenta esto. Por tal razón fallara.

El segundo caso de la definición es el típico de apartamentos y escuelas porticados que se les añade un muro debajo de las ventanas, entre columnas, rellenando el espacio, es decir pegado a las columnas. Cuando la estructura es excitada por un sismo el muro empotra la parte de la columna a la que está conectado y la columna queda libre solo por encima del alfeizar lo que ocasiona que cuando el Diafragma le transfiere desplazamiento se crea una distorsión angular ya que el muro es más rígido y la columna fallara por cortante al ser golpeada en la zona del alfeizar. Luego del movimiento de la columna esta quedara degradada en su rigidez y las cargas verticales quedaran excéntricas y harán fallar por aplastamiento la columna.
Veamos varios ejemplos para una mejor y más profunda comprensión:
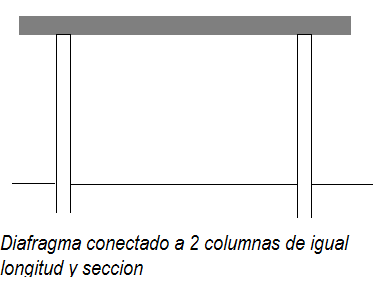
En la gráfica tenemos dos columnas iguales de sección y longitud. Cuando el Diafragma recibe la excitación lateral se desplaza horizontalmente y empuja las dos columnas que se desplazaran igual.
Recordemos que de la Física, F=K.x à x =F/K como K= nEI/L³ (Para simplificar tomaremos n=1).
x = F.L³/E.I como F,E e I son Iguales nos queda x=L³, o sea que el desplazamiento aumentara en proporción a la longitud.
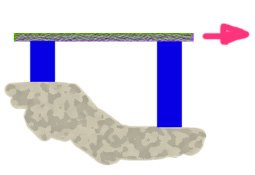
Si ahora tomamos una de las columnas y la enterramos, una parte de su longitud que está enterrada funcionara como empotramiento y entonces la longitud de la columna será una fracción de la original. Si enterramos la ¾ partes nos quedara una longitud de columna de ¼.L por lo que la nueva rigidez será K=nEI/(0.25L)³ = 64EI/L³. Esto último significa que la rigidez aumenta 64 veces para la misma sección de columna al ser enterrada ¾ veces su longitud.
Creo que con este ejemplo quedara claro el concepto de Columna Corta. Sin embargo mostraremos otro ejemplo para que quede claro como la diferencia de rigidez afecta el desplazamiento.
Tomemos las mismas columnas con la misma longitud pero ahora una tendrá sección de 1.00×1.00 m2 y la otra 0.50×0.50 m2.
La inercia de la primera será: 1×1³/12 = 0.0833 m4
La inercia de la segunda será: 0.50×0.50³/12 = 0.0052 m4
Si dividimos la mayor inercia entre la menor veremos que la inercia de la mayor es 2E4 = 2x2x2x2 = 16 veces o 0.0833/0.0052 = 16.
Como las longitudes son iguales las cambiaran igual.
Mas adelante continuaremos tratando el mismo tema pero en otros tópicos similares como:
-Piso Debil.
-Piso Suave.
-Irregularidades en altura y horizontal.
-Cambios de masa.
-Masas concentradas.
-Etc.




Comments (16)
Yuri Villavicencio-Fdez - 14 septiembre, 2011
Excelente post. Muchas Gracias Ingeniero!
Jose Rafael Cabrera Sepulveda - 14 septiembre, 2011
Es un placer. Vamos a repasar en los siguientes dias todas los topicos que deben evitarse en la estructuracion sismorresistente.
Ezequiel - 14 septiembre, 2011
Muy buen aporta Ingeniero, sobre columnas cortas, me gustaria que pusiera sobre las losas piso suave y debil..
Estare al tanto de que publique eso..
Gracias
Jose Rafael Cabrera Sepulveda - 14 septiembre, 2011
Ezequiel, muy agradecido por tu comentario.Como escribi, esta sera una secuencia de articulos que se en focaran primero en los distintos aspectos a evitar con sus caracteristicas. Luego escribiremos otra serie de articulos sobre soluciones y reparaciones o retrofitt cuando ya esten hechas las edificaciones.
Geraldo Pineda - 14 septiembre, 2011
Buen post. Soy estudiante de Ingenieria Civil y precisamente estoy viendo diseño de columnas.
Gracias Ingeniero
Jose Rafael Cabrera Sepulveda - 14 septiembre, 2011
Gracias Geraldo. Debo observar que cuando hablamos de Rigidez lateral, indirectamente estamos hablando de Esbeltez. (a proposito del comentario de Geraldo).
Jose Rafael Cabrera Sepulveda - 14 septiembre, 2011
Ezequiel, se le llama piso o losa suave, debil pero no es un problema que se origina en la losa sino en la rigidez o en la resistencia de las columnas comparadas con las de los pisos adyacentes.
NORMAN ALVARADO RODRIGUEZ - 15 septiembre, 2011
Muy ilustrativo el tema , y le agradezco mucho Ingeniero por su aporte a los conocimientos de Ingeniería Civil, sobre todo en el diseño sismoresistente de columnas, aprovecho para hacelre la siguiente pregunta:
Cual es el comportamiento de un sobrecimiento de 1.50m de altura de 0.12m y 0.23m de espesor deseo saber cual sería el área de acero en malla(vertical y horizontal)
Ing. José Cabrera - 15 septiembre, 2011
Gracias Norman .Me imagino que le llamas sobrecimiento al pedestal o columna corta. Me lo imagino por la altura de 1.50 m. Pues el Diseno de cualquier elemento estructural depende de las solicitaciones a que estara sometido asi como a las propiedades mecanicas de los Materiales. Lo que hay hacer que primero es tener esos datos y con ellos proceder a disenar el elemento.
PEDRO BALLENA - 16 septiembre, 2011
en la grafica se observa el cso tipico de vanos de crujias de edificios de aulas
que se han construido en el Peru( Infes), la columna corta se elimina si de independiza el muro de albañileria de las columnas de los porticos contiguos (junta)
Jose Rafael Cabrera Sepulveda - 16 septiembre, 2011
Pedro gracias. Fijate que en esta etapa estamos solo definiendo las Patologias. Cuando terminemos con todas las Patologias pasaremos a los estudios de vulnerabilidad y las diferentes formas de solucion.
CivilGeek - 20 septiembre, 2011
Excelente aporte… entendido el tema de columnas cortas.
Bolivar - 16 octubre, 2011
Resulta dificil encontrar un profesional de su experiencia y con una comprension muy cercana a lo exacto sobre la transmision de conocimientos en la ingenieria civil, le sugiero desglosarnos el asunto de la comprension del grafico aceleracion -tiempo; veloc-tiempo y desplaz-tiempo, asi como la contruccion del grafico aceleracion espectral de referencia y diseno…..pues algunas normas no son muy explicitas.
Creo firmemente que la educacion debe ser gratuita y el trabajo bien pagado para mejor avance de la humanidad.
Bolivar - 16 octubre, 2011
Me perdona usted pero quisiera irme mas lejos:
Soy Ing. Dominicano como usted, interesado en sismologia y sismoresistencia y entiendo que debemos hacer un mayor esfuerzo, primero para ampliar la cultura sismica del ciudadano comun y a la vez elevar los conceptos tecnico entre los profesionales de la ingenieria, compartiendo los conocimientos, en esa linea estoy dispuesto a continuar capacitandome y participando para servir(en ambas vertientes), dado el hecho que debemos esperar acontecimientos como el de Haiti y es justo avanzar ahora para evitarnos males mayores, semejanta a lo ocurrido alli.
Gracias por sus sanos y bien intencionados aportes.
Bolivar Nova
Codia 2951
Jose Rafael Cabrera - 16 octubre, 2011
Gracias Bolivar, lo que ocurre con toda la informacion que leemos es que esta escrita para que la lea el que lo escribio. Te prometo que cuando tenga un tiempo libre escribire
sobre el tema que me senalas.
Luis Anchundia - 17 junio, 2014
excelente aporte ingeniero… muy entretenido, si podría facilitarme alguna referencia bibliográfica o si hay conoce de alguna investigación acerca del tema para empaparme mucho mas en el tema y profundizar mas en lo que es columnas cortas me seria de gran ayuda.