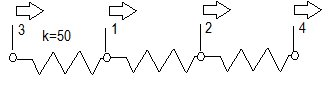
Veamos un caso más general. Cada resorte tiene k=50 lb/pulg. La numeración esta hecha para simplificar el trabajo.
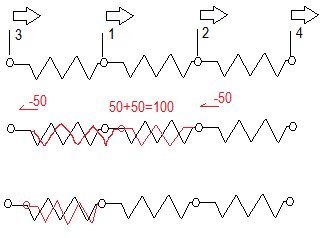
Vamos a generar los coeficientes correspondientes a la primera columna de la matriz de rigidez. Desplazamos la coordenada 1 una unidad hacia la derecha al aplicar una fuerza de 100 lb y todos los nudos restantes los mantenemos en su lugar. Porque 100 lb y no 50 lb? Porque al desplazar el nudo 1 tendremos que vencer las constantes de dos resortes (3-1 y 1-2). El resorte izquierdo tendrá una fuerza a tensión de 50 lb y el de la derecha tendrá una fuerza a compresión de 50 lb. Para mantener el equilibrio debemos colocar una fuerza contraria en cada nudo de 50 lb.
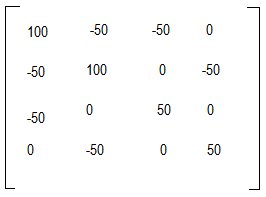
La primera columna con sus coeficientes de rigidez serán:
Estos coeficientes (k11,k21,k31,k41) representan las proporciones de las constantes de resortes que participan en la respuesta a la carga colocada para provocar el desplazamiento unitario en 1. Observar que si la numeración o la carga hubiera cambiado la columna no seria igual pero al final se lograría el mismo objetivo.
Si aplicamos la misma metodología en el nudo 2 la columna será:
K12 es el coeficiente en el nudo 1 debido a la carga en 2 (-50). K22 es la carga en 2 para generar el desplazamiento unitario en 2. K32 es cero porque a este nudo no llega el efecto de la fuerza en 2 porque al estar fijo el nudo 1 no le llega desplazamiento. K42 es -50 porque es la reacción contraria de ese resorte que junto a k12 equilibran la fuerza.
En los demás casos es mas sencillo, por ejemplo, al coloca 50 lb en 3 para provocar un desplazamiento a la derecha de 1 pulg tendremos en 1 una reacción contraria de -50 donde el nudo esta restringido pero le llega al resorte la demanda del desplazamiento; en dos será 0 y en 3 ponemos la solicitación de 50:
En el nudo 4 hacemos igual y tendremos:
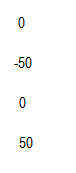


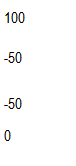
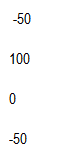
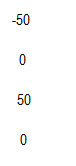
Comments (3)
Mariano - 22 febrero, 2012
Muchas gracias por sus aportes Ing. José Cabrera.
Por favor siga contribuyendo a la formación de los Ing. Civiles.
adeluna100 - 22 febrero, 2012
Mil gracias por el aporte.
Anthony Frank - 28 julio, 2014
Muchas gracias por el gran aporte Ing. José. Muy entendible y quedaríamos muy agradecidos si nos diera más enseñanzas básicas de análisis estructural.