La Gran pirámide de Guiza es la más antigua de las Siete maravillas del mundo y la única que aún perdura, además de ser la mayor de las pirámides de Egipto. Fue ordenada construir por el faraón de la cuarta dinastía del Antiguo Egipto Keops. El arquitecto de dicha obra fue Hemiunu.
Pirámide de Guiza
La fecha estimada de terminación de la construcción de la Gran Pirámide es alrededor de 2570 a. C., siendo la primera y mayor de las tres grandes pirámides de la Necrópolis de Guiza, situada en las afueras de El Cairo, en Egipto. Fue el edificio más alto hasta el siglo XIV (siendo superado por el chapitel de la Catedral de Lincoln, en Inglaterra y el edificio de piedra más alto del mundo hasta bien entrado el siglo XIX, siendo entonces superado por la aguja de la iglesia de San Nikolai, en Hamburgo.
La pirámide
Fue construida con unos 2.300.000 bloques de piedra, cuyo peso medio es de dos toneladas y media por bloque, aunque algunos de ellos llegan a pesar hasta sesenta toneladas. Originalmente estaba recubierta por unos 27.000 bloques de piedra caliza blanca, pulidos, de varias toneladas cada uno. Mantuvo este aspecto hasta principios del siglo XIV, cuando un terremoto desprendió parte del revestimiento calizo. Posteriormente, los turcos otomanos utilizaron dicho revestimiento para la construcción de diversas edificaciones en El Cairo.
Datación
Los egiptólogos, arqueólogos especialistas del Antiguo Egipto e historiadores (desde Heródoto) , coinciden en afirmar que fue construida durante el reinado de Jufu (Keops), en la primera mitad del siglo XXVI a. C.. Se piensa que su construcción fue dirigida por su chaty, el arquitecto Hemiunu.
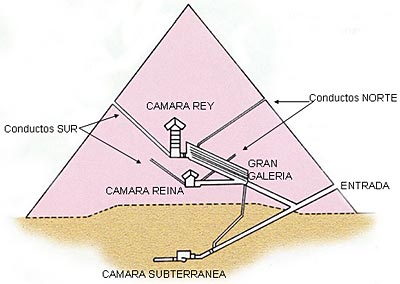
El interior de la pirámide
La pirámide se compone de tres cámaras principales, dos situadas en el interior de la pirámide, actualmente denominadas Cámara del rey y Cámara de la reina, y una en el subsuelo, la Cámara subterránea.
A las cámaras se accedía desde el lado norte, por un pasaje descendente, obstruido al final por grandes bloques de granito, que comunicaba con dos pasadizos, uno ascendente, que desemboca en la Gran galería, y otro descendente, que llega hasta la Cámara subterránea.
La Gran galería
La Gran galería es un gran pasaje ascendente de unos 47 metros de longitud y ocho metros de altura. Las paredes de la Gran galería son planas hasta una altura de dos metros y, a partir de ahí, escalonadas, conformando una falsa bóveda por aproximación de las hiladas.
La Cámara del rey
La Cámara del rey está conformada por losas de granito y es de planta rectangular, paredes y techo lisos, sin decoración, y únicamente contiene un sarcófago vacío de granito, sin inscripciones, depositado allí durante la construcción de la pirámide, puesto que es más ancho que los pasadizos; sobre el techo se encuentran las llamadas cámaras de descarga, y la más alta dispone su techo con grandes bloques inclinados, a dos aguas, para desviar la gran presión que ejercen los bloques superiores de la pirámide, evitando que todo el peso descargue sobre el techo de la cámara real. Se accede a ella por un pasaje horizontal llamado antecámara que parte del extremo superior de la Gran galería.
La Cámara de la reina
La Cámara de la reina, denominada así por los árabes, aunque según Mark Lehner y la gran mayoría de los egiptólogos, no se destinó a la esposa del rey sino a una estatua Ka del mismo (Serdab, habitáculo destinado a contener la representación espiritual del difunto: estatua Ka), está situada casi en el eje de la pirámide; tiene acceso mediante un pasaje horizontal, que comunica con la zona inferior de la Gran galería, inicialmente oculto por las losas del pavimento. Es de planta rectangular, paredes lisas, sin decoración, con un nicho, y techo inclinado, a dos aguas.
La Cámara subterránea
La Cámara subterránea, excavada en el subsuelo, es de planta rectangular, con suelo irregular, paredes y techo planos; contiene dos habitáculos, a modo de sarcófagos, un pozo y una pequeña galería. Se accede a ella por un pasaje descendente, que es prolongación del primer pasillo de la pirámide. También está comunicado con la Gran galería mediante un angosto túnel, casi vertical, perforado en los bloques.
Los canales de ventilación
De cada cámara real parten dos angostos conductos inclinados, en las paredes norte y sur, llamados «canales de ventilación», pues ese es su uso actual, ventilar mediante impulsores eléctricos; se desconoce su función original pues los de la Cámara de la reina no comunicaban con el interior en su último tramo, ya que estaban tapados por las grandes losas graníticas del revestimiento de los muros. Los de la Cámara rey fueron descubiertos por R. Howard Vyse, y los de la Cámara de la reina por W. Dixon.
Sección Sur-Norte.
Cámaras y pasajes interiores
- Acceso original, en la cara norte, actualmente obstruido
- Acceso actual, ordenado abrir por Al-Mamun
- Bloques de granito, sellando el acceso al pasaje superior
- Pasaje que comunica con la Cámara subterránea
- Cámara subterránea
- Pasaje de acceso a la Gran galería
- Cámara de la reina
- Pasaje que comunica con la Cámara de la reina
- Gran galería
- Cámara del rey y cámaras de descarga
- Antecámara
- Pasaje perforado que comunica con la Gran Galería y la Cámara subterránea
- 7-10 Canales de ventilación
¿Quién y cómo construyeron las pirámides?
La fascinación que despierta un monumento tan antiguo y singular como la Gran Pirámide de Keops ha dado lugar a las más diversas interpretaciones fuera del estricto ámbito de la arqueología. Unos piensan que se trata de una gigantesca biblia de piedra, cuyos elementos arquitectónicos esconderían, codificados, arcanas revelaciones de carácter iniciático. Otros creen que fue construida con ayuda de tecnología extraterrestre y que estaba destinada a servir, en esos tiempos remotos, de punto de referencia para el aterrizaje de potentes naves interestelares.
Ante una obra humana de semejante calibre, tan grande y tan absolutamente resistente al paso del tiempo, continúa siendo inevitable preguntarse (al igual que hiciera Herodoto y luego Napoleón) cómo fueron levantadas las pirámides, y sobre todo, por qué. Y es que el inmenso esfuerzo que supuso extraer, transportar, tallar y encajar cada uno de los bloques no hubiese sido posible sin una fuerza espiritual que impulsase los músculos y la voluntad de los trabajadores en la erección de esta magna construcción, la más imponente de toda la historia de la humanidad.
Muchos son los cálculos y cifras barajados por los especialistas acerca de las pirámides de la IV dinastía. Durante los cien años de historia egipcia que corresponden al periodo de su construcción, se tuvo que colocar un bloque de piedra cada cuatro minutos y medio, con un promedio de 2500 kilos por bloque. En total, 8.972.500 metros cúbicos y 12.000.000 de bloques manipulados entre 25.000 personas trabajando una jornada de 10 horas diarias. Lo que era imposible con la tecnología de la Edad de Piedra. La más convincente de las teorías es una rampa que giraba en espiral alrededor de la pirámide. Los bloques se remolcaban sobre los trineos hasta el punto más alto, pero construir esta rampa sería más difícil que construir la pirámide. Todavía sigue siendo un misterio como lograron determinar la planta de la Gran Pirámide de Guiza con tanta exactitud. Según los cálculos modernos, los ángulos entre cada dos lados de la base miden 89 grados, 59 minutos, 5 segundos; y 90 grados, 0 minutos y 58 segundos respectivamente. Tamaña precisión en la búsqueda del ángulo recto permitió que los cuatro lados fueran absolutamente iguales, o casi. En realidad tienen una desviación máxima de 5 centímetros, sobre una longitud total de 230 metros por lado. Nadie sabe cómo fueron extraídas las piedras de las canteras para la construcción de estas pirámides. Dice una extraña leyenda árabe que, para construir la Gran Pirámide, se colocaban bajo las piedras unas hojas de papiro en las que había escritos mensajes secretos. Tras ser golpeadas por una varita, las piedras iban ascendiendo por el aire hasta situarse cada una en su lugar.
La geometría sagrada
La opinión unánime de todos los arquitectos e ingenieros que han estudiado la Gran Pirámide es que su construcción obedece a un replanteo. Es decir, de los planos de dibujo se pasó a la edificación, eliminando cualquier teoría que pretenda indicar que se pusieron a subir bloques de manera arbitraria. Esos planos fueron concebidos siguiendo los conceptos que el arquitecto quiso incorporar y la función de la piramidología consiste precisamente en adivinar dichos planteamientos, ya que las medidas de la Gran Pirámide fueron proyectadas bajo un criterio arquitectónico, como cualquier edificio actual. Los arquitectos, tras realizar los estudios pertinentes, pueden llegar a averiguar cuáles fueron esos planteamientos. Otra cosa es jugar con los números para hallar un carnet de identidad, un número de teléfono o cualquier otro malabarismo intelectual. La ciencia es otra cosa.
Vamos con las medidas de la Gran Pirámide. Pongamos que aproximadamente la base mide 230,30 metros, que la altura original era de 146,6 y la apotema de sus caras (la línea que recorre todo el centro de la cara) es de 186,3. Pues bien, si simplificamos estas medidas y consideramos que la base mide 2, la altura mediría 1,272 y la apotema sería 1,618. Es decir, un triángulo que tenga como base 2, como altura 1,272 y como los lados 1,618, tendría las mismas proporciones que la Gran Pirámide en su corte transversal. La altura divide a ese triángulo en dos triángulos rectángulos menores que tendrían como base 1, como altura 1,272 y como hipotenusa 1,618.
O sea, que la Gran Pirámide está edificada teniendo como armazón a un triángulo rectángulo que tiene como base la unidad de medida, como altura la raíz del número Fi (1,618). Por lo que queda demostrado que el número Fi está incorporado a la Gran Pirámide sin distorsionar ninguna medida. Por si acaso hubiera dudas, la secante del ángulo de 51 grados y 51 minutos (ángulo de inclinación de la Gran Pirámide) es 1,618 (Fi) y por ende el coseno de 51 grados y 51 minutos es el inverso de Fi (0,618).
Las medidas de la Gran Pirámide resuelven la cuadratura de la circunferencia. Demostración: La circunferencia que tiene como radio la altura de la pirámide tiene la misma longitud que la base cuadrada de la Gran Pirámide.
Radio = 146,6 x 2Pi = 921
Lado de Base = 230,30 x 4 = 921
Lo cual implica que si dividimos la base de la pirámide por el doble de la altura obtenemos el número Pi.
Las medidas de la Gran Pirámide resuelven la cuadratura del círculo. Demostración: un rectángulo formado por la base de la Gran Pirámide y su altura tiene la misma superficie que un semicírculo que tenga como radio la altura de la pirámide.
Superficie del semicírculo = Pi x radio2 /2 = 33.758
Superficie del rectángulo = 230,3 x 146,6 = 33.761
Las medidas de la Gran Pirámide resuelven la cubicación de la esfera. Demostración: según la geometría, la mitad de un círculo plano es también matemática y rigurosamente igual en área a la superficie esférica de un cuadrante de 90 grados. O sea, que un rectángulo cuya altura y base sean las de la pirámide tiene la misma superficie que un cuadrante esférico cuya altura sea la de la pirámide y su arco la base de la Gran Pirámide.
Superficie del cuadrante esférico = arco x radio = 230,3 x 146,6 = 33.761
Superficie del rectángulo = 230,3 x 146,6 = 33.761.
Otra demostración: la superficie del prisma generado tomando la base y la altura de las caras de la Gran Pirámide (una caja donde se pudiera meter la Gran Pirámide) tiene la misma superficie que la semiesfera generada tomando como radio la altura de la Gran Pirámide.
Base x altura 230,3 x 146,6 x 4 caras = 135.047
Superficie de la semiesfera = 4 x Pi R2 / 2 = 4 x Pi x 146,6 x 146,6 /2 = 135.035.
Ahora nos enfrentamos a un problema con dos posibles soluciones:
1. Los constructores de la Gran Pirámide adquirieron en tiempos de Keops el conocimiento de los números Pi y Fi e inmediatamente después se olvidó en Egipto tal conocimiento, en una absoluta pérdida de memoria sin parangón conocido en la historia de la ciencia.
2. Los egipcios, que desconocían estas proporciones, no pudieron construir ni siquiera el boceto arquitectónico de la Gran Pirámide. Pero esa es otra historia.
Los constructores ocultos
Desde la más remota antigüedad todos los hombres de ciencia miraron a la Gran Pirámide como poseedora de informaciones referentes a las medidas terrestres y celestes. Y, posiblemente, tales datos se hallen incorporados en sus proporciones.
Pero hay más. El premio nobel Linus Pawling demostró que la molécula de agua no es H2O, sino un polímero formado por 5H2O. El eminente científico afirmó asimismo que la forma de la molécula del agua corresponde a una pirámide de base cuadrada, en cuyas cinco esquinas se situaría un H2O, y que el ángulo de esta formación era 52º.
Con este dato podemos afirmar que la Gran Pirámide es el mayor monumento construido a la molécula del agua. Pero, curiosamente, el único mineral cuya cristalografía corresponde exactamente a la geometría de la pirámide es el diamante, el carbono puro, con lo que tenemos que el agua y el carbono, los principales elementos que componen el cuerpo humano se hallan representados en este singular monumento. Quizás sea casualidad, pero el número de hiladas de la pirámide corresponde al número de huesos que tiene el ser humano, 204. Y podría seguir enumerando «casualidades» que indican que, por un lado, la Gran Pirámide es el mayor compendio astronómico escrito en piedra pero, por otro lado, representa al ser humano en toda su extensión, física y espiritual.
Quizás sea por ello que en el interior de la Gran Pirámide nos sentimos afectados. Su geometría sagrada influye en los organismos y provoca una energía sutil capaz de alterar los instrumentos electrónicos de medida. Algunos consideran que la Gran Pirámide actúa como una antena emisora-receptora de sensaciones e informaciones.
Quién sabe. No existen pruebas categóricas para responder a la pregunta de quiénes fueron esos seres superiores que edificaron la Gran Pirámide. Lo que sí sabemos es que la tecnología y los conocimientos empleados en su construcción no estuvieron al alcance de los egipcios de la IV Dinastía. O, por lo menos, que no deberíamos clasificar tan superficialmente un monumento que se ríe del tiempo y de todos los que aventuramos nuestras temblorosas hipótesis porque, en este momento, no sabe más sobre la Gran Pirámide el que más respuestas aporta, sino el que más preguntas se hace.
EL METRO SAGRADO EGIPCIO
Y todo lo contrario. Como primicia mundial vamos a demostrar que el metro real egipcio se corresponde con medidas geodésicas de nuestro planeta, de una forma absolutamente constatable. Partimos de la esfera ideal cuyo radio es el radio de la Tierra medido en Giza. Pues bien, la longitud de arco comprendida entre la Gran Pirámide y el polo norte de dicha esfera corresponde a la cifra de 6.673,611 km. Todo este planteamiento nos lleva a dar una simple fórmula que dictamina milimétricamente y con datos geodésicos absolutamente fiables el metro utilizado en la Gran Pirámide:
1 metro egipcio = Radio en Giza x W/60.QOO
Es decir: 6.372,829 x 3,14162/60.000 = 1,048.
Para los amantes de la geometría, se cumple también que la diezmillonésima parte del cuadrante del meridiano de una esfera con radio de 6.673,611 km., sería, precisamente, 1,048 metros, el patrón de medida utilizado en la Gran Pirámide.
Estamos seguros de que estos datos, que publicamos por primera vez, aunque difícilmente comprensibles para los neófitos en geometría y en astronomía, revolucionarán la historia de la piramidología, al relacionar el metro sagrado egipcio, empleado en todas las medidas interiores y exteriores del monumento, con datos geodésicos intrínsecos a la ubicación de la Gran Pirámide en nuestro planeta. Este monumento señala un punto exacto de la superficie terrestre, el mismo punto desde donde se sospecha que alguien situado a unos 10.000 metros de altura pudo tomar una imagen, por métodos desconocidos, del globo terrestre. Aquellas remotas observaciones se plasmaron en antiguos mapas como el de Piri Reis, distorsionado con asombrosa exactitud debido a la falta de concavidad de la fotografía original. Un punto geodésico que señala que los constructores del monumento y, posiblemente, los instructores de los pueblos de la antigüedad, conocían las medidas de nuestro planeta, porque eran poseedores de una tecnología ajena y avanzadísima, sin la cual no podrían haber llegado de ninguna forma a conseguir estos datos.
UN INSÓLITO DESCUBRIMIENTO
Pero hagamos el proceso contrario. Supongamos que queremos construir el monumento más grande de la Tierra, que disponemos de toda la tecnología precisa para tal fin y que queremos incorporar las medidas del planeta a esa pirámide. Partimos de la premisa constatada de que la Tierra no es una esfera perfecta. La figura geométrica que mejor define la superficie de nuestro planeta es un elipsoide de revolución, es decir, un cuerpo engendrado por una elipse, cuyos ejes son los radios polar y ecuatorial, y que gira sobre el radio polar. Actualmente, la geodesia física hace un estudio de la Tierra considerándola un geoide, definiendo su superficie como la de los océanos en calma y los continentes sin tener en cuenta su relieve, es decir, como si toda la tierra estuviese al mismo nivel del mar. Si superponemos las figuras elipsoide y geoide de la Tierra (como si superpusiésemos, por ejemplo, un melón y una sandía), ambas coincidirán en determinadas líneas, que consideraremos «zonas de cota cero».
Queremos, pues, construir una pirámide que cumpla dos condiciones. La primera es que esté situada en el meridiano terrestre donde interseccionen el elipsoide y el geoide antes mencionados (ver figura). Para ello, nos basaremos en un mapa que representa estas dos superficies y sus discrepancias, publicado en el libro Geodesia Física de Weikko A. Heiskanen, donde figuran los antes mencionados puntos de intersección o líneas de cota cero. En él podemos ver que los únicos lugares del planeta donde se cumple esta primera condición son una franja de terreno que recorre el Nilo y otra que, subiendo por la cuenca del Amazonas, llega a la península del Yucatán y a México, siendo exclusivamente la zona de Egipto donde la línea que tiene cota cero en todos sus puntos coincide con el meridiano del lugar.
La segunda condición es que el lugar preciso del emplazamiento de dicha pirámide esté ubicado en aquel paralelo cuyos puntos estén situados en su totalidad a la misma distancia del Polo Norte y del centro de la Tierra. Con ello, obtenemos un solo punto en el planeta que cumpla estas dos premisas: la meseta de Giza, situada en el paralelo 29° 58′ 51″ norte y longitud 31 ° 9′ este de Greenwich.
Asombrosamente, cada punto de la Tierra tiene un radio diferente, debido al achatamiento de los polos. El radio polar –según el anuario del Observatorio Astronómico, que publica las medidas dadas por el Servicio Internacional de la Rotación Terrestre (IERS)– es de 6.356,751 km, siendo el radio ecuatorial de 6.378,136 km. El radio terrestre en la meseta de Giza es de 6.372,829 km.
Hasta hoy se ha especulado mucho en relación con la unidad de medida empleada en la Gran Pirámide. El problema principal reside en la diferencia entre nuestro metro actual, la diezmillonésima parte del cuadrante del meridiano que pasa por Dunkerke y Barcelona, y el metro real egipcio, estimado por el notable egiptólogo Petrie en 1,0479 y por Newton en 1,0478. Por ello han surgido algunas teorías extravagantes que han tratado de hacer coincidir nuestro metro actual con el utilizado en el antiguo Egipto como, por ejemplo, prolongar el radio polar «convenientemente» 300 kilómetros, para elevar nuestro vulgar 1,00 a la categoría de 1,048, definiendo la atmósfera con ese exacto espesor, como si ésta fuese uniforme. Por tanto, los estudiosos más oficialistas han tomado a broma siempre tales consideraciones, afirmando que el metro egipcio no podría corresponderse con dato geodésico o astronómico alguno.
VIDEO EN 3D:
http://www.3ds.com/3dexperience/passion-for-innovation/khufu-reborn/khufu-reborn/
SUMINISTRADO:
Created By: Ing. Nestor Luis Sánchez – Tw:
@NestorL


![[imagenes.4ever.eu] piramides de giza 152364](https://civilgeeks.com/wp-content/uploads/2013/10/imagenes.4ever.eu-piramides-de-giza-1523641-720x422.jpg)






Comments (5)
adeluna100 - 13 noviembre, 2013
Mil gracias por la información.
William Clavijo Robinson - 3 noviembre, 2015
Resumen Datos y Cálculos utilizados en Pirámides Kefrén y Giza
7*4 = 28 * 10 = 280
Constelaciones = 88 (22*4 = 88)
Misterioso = 123
Codo Egipcio = 0,5236
Pi (π) = (Codo Real Egipcio) por 6 = 0,5236 * 6 = 3,14160000000
Phi (φ) = (0,5236*5)-1 = 1,618
123 * 7 = 861 (perímetro Kefrén)
Altura Kefrén (metros) = 861/6 = 143,5
Base Kefrén (metros) = 861/4 = 215,25
Base sobre altura (b/h) = 215,25/143,5 = 1,5
Altura Kefrén (codos) = 143,5/0,5236 = 274,064171122995
Altura/2 (codos) = 137,032 (La energía electrónica de carga es 137 veces la energía del fotón)
Apotema = 179,376.
Ángulo Sagrado Egipcio = 53º 7′ 48,368” (realmente sagrado)
Perímetro Kefrén (metros)/altura (codos) = 861/274,064171122995 = 3,14160000000
Base Giza (codos) = 440
Altura Giza (codos) = 280,112
(b/h)*2 = (440/280,112)*2= 3,14160000000
Altura Giza (metros) = 146,667
Base Giza (metros) = 440*0,5236 = 230,384
Pendiente Giza = 280,112/220 = 1,273236567
Ángulo de inclinación = 0,905021441 = 51,854º = 51º 51′ 14″
Ángulo Complementario = 38,146º
Numero de Euler = (Ángulo de inclinación/Ángulo Complementario) * 2 = 2,718
Superficie de caras triangulares de la pirámide = (b/2 * h)*4 = 246498,5994 codos
Superficie del círculo formado tomando como radio de la altura = 246498,5994 codos
Conclusión: Lo anterior significa que lo egipcios trabajaron como hoy en día con un Pi redondeado de 3,1416 ya que este valor está inmerso en su sistema de medición, el codo real egipcio (3,1416/6 = 0,5236) y conocían perfectamente el teorema de Pitágoras demostrado en su ángulo sagrado, y el numero aúreo (Phi) todo con límites prácticos (1,618). El número aúreo Phi también está inmerso en el codo real egipcio (0,5236*5)-1 = 1,618. Las coincidencias del número 137 y el número de Euler son enigmáticas. (Central electromagnética de fotones?). Tanta elegancia no puede ser coincidencia. Nada ocurre por casualidad, pero si por casualidad. Puede ser que desde las Pirámides se comunicaban con Orión vía Satélite.
William Clavijo Robinson - 10 noviembre, 2015
Pirámide de Keops (Jufu) – Phi (φ) – Pi (π)- La Cuadratura
Base en codos: 480 codos
Base en metros 230,38 m
Altura en codos: 280 codos
Altura original Giza en metros: 146,608 m = (146,61)
Phi (φ) = (146,608/280)*5) – 1 = 1,618
Pi (π) = (280/146,608)*2 = 3,1416
Pirámide Kefrén
Constante de estructura fina α-1 = 137,035999710(96)
Pi (π) = 3,14159265358979
Constante de estructura fina α multiplicada por Pi (π) = 430,51129
430,51129/2 = 215,255645 m = base pirámide Kefrén
430,51129/3 = 143,503763 m = altura pirámide Kefrén
Vaya Coincidencia
William Clavijo Robinson - 20 noviembre, 2015
Pi (π) Presente en la Pirámide de Kefrén
Las dimensiones de la pirámide Kefrén fueron calculadas en base a Pi (π)
Misteriosos primos: 3 * 41 = 123
Sagrado 7: 123 * 7 = 861m (Perímetro Kefrén)
Base: (861 m / π/6) /4 = 411,097218006366 codos
Base: 411,097218006366 codos * π/6 = 215,25 metros
Altura: 861 m / π = 274,064812 codos
Altura: 274,064812 codos * π/6 = 143,5 metros
William Clavijo Robinson - 1 diciembre, 2015
Simplemente esto
Pi/2 * (10 * ((7 * 4 + /(PI/7)/4^2*10))*4) = 439,999 (Base Keops codos)
10 * ((2Pi * 7) /Pi/2) = 280 codos (Altura Keops)
2 es el diámetro del círculo
4 es el área del cuadrado circunscrito al círculo unitario
1 es el radio
El perímetro es = 8
El perímetro menos el radio = 7
10 es el factor de Escala
Pi en Kefrén
123 * 7 = 861m (Perímetro Kefrén)
Base: (861 m / π/6) /4 = 411,097218006366 codos (Base en codos)
Base: 411,097218006366 codos * π/6 = 215,25 metros (Base en metros)
Altura: 861 m / π = 274,064812 codos
Altura: 274,064812 codos * π/6 = 143,5 metros
Pi = 861 / 274,064812 = 3,14159265358979
Pi (π) en Mycerinus
Base Menor Pirámide = 335 pies = 102,108 metros
102,108 metros * π/2 = 65 metros (Altura Mycerinus)
Cinco Aproximaciones rápidas de Pi con 14 dígitos (Rectificación)
1. 3 +√2/10 + (√2/2 +1)/10^4 + (√3/2 +5)/10^7 + ((√√2 + 6) +7/10^3)/10^11 = 3,14159265358979
2. (7 +1/10) / ((9 + 4/100)/4) – ((8/√2) – 3) + 1/100)/10^7) – 1/(√1,25 + √0,5 + √2 + √3 + √5 + √7 + √8)*10^10 + (√3/2)/10^14 = 3,14159265358979
3. 6*((√1,25 +1,5)/5) – (2 + √8)/10^5) + (4/√7)/10^7 + 1/ (√√8 +10)*10^10
4. + 1 / (√1,25 – 4/1000)/10^10 = 3,14159265358978
5. 4*(0,5 + ((√0,5 +5)/10)/2) + ((2 + √0,5) + 1)/10 + (1 / (√7/10)) /10^4 + (√5/10 + √2)/10^6 + (2/√7)/10^10 + ((8 + √7) – 0,5)/10^12 = 3,14159265358979
6. √8 + 0,25 + 0,0625 + (1 /(150 + ((√7 + 3)/10) + 2)/10)*10) + 1 / (√0,5/3)*10^11
7. + 1 /(7 + √5) / √7)*10^12 = 3,14159265358979