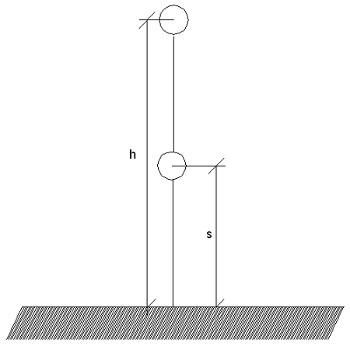
Supongamos que desde cota cero lanzamos una partícula verticalmente hacia arriba con una velocidad “V0″ (una velocidad tal que el movimiento subsiguiente se encuentre en el rango que permite considerar la aceleración de la gravedad “g” constante). La partícula sube, baja y rebota contra el suelo de tal modo que en cada impacto pierde LA MITAD de la energía cinética que traía.¿Cuánto tiempo tardará en parar?
Finito y lo Infinito
En primer lugar, si en cada rebote pierde la mitad de su energía cinética, la relación entre las velocidades de dos ciclos consecutivos es:
En uno cualquiera de los ciclos, si aplicamos la ecuación de las velocidades con aceleración «-g» y considerando que la velocidad de llegada es la de salida con signo contrario:
Podemos ahora referir cada velocidad a la inicial y cada tiempo a esta misma velocidad:
Y se observa una relación de los subíndices con las potencias, con lo que podemos expresar el tiempo total como la suma de los tiempos:
El sumatorio infinito se ha resuelto sabiendo que es una serie geométrica, con su fórmula de suma, pero si uno no se acuerda en un momento dado, siempre puede sumarse por «instinto». Veamos como.
Vamos a expresar el sumatorio desarrollado
Multiplicamos todo por 1/√2 y queda:
Restando ambas expresiones miembro a miembro nos damos cuenta de que los puntos suspensivos son innecesarios:


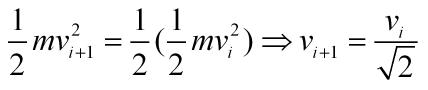
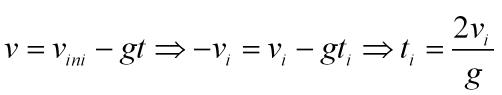
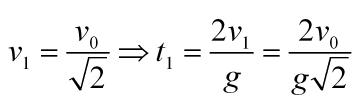
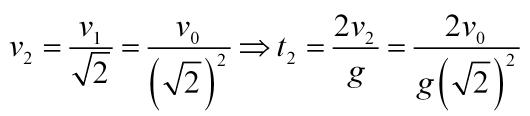
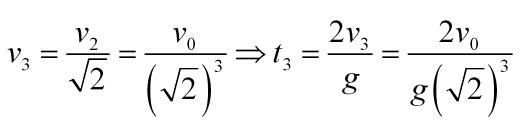
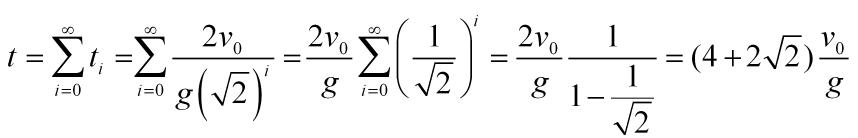
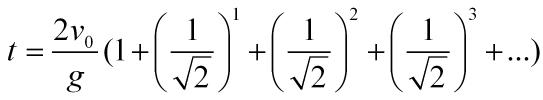
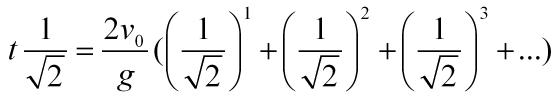
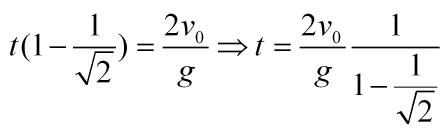
Comments (2)
Alejandro Marin - 16 febrero, 2012
Excelente ejercicio propuesto, este problema me recuerda mucho los primeros años como estudiante de ingeniería, resultan excelentes para introducir al estudiante a la materia del calculo matemático. Seria muy provechoso un articulo sobre series de Fourier.
Saludos.
Gustavo - 27 julio, 2014
Estimado, solo un comentario: en la resta de las dos expresiones al final, quedan dos terminos que no se anulan: (1/raiz(2))^n-(1/raiz(2))^(n-1). Sin embargo, cuando n tiende a infinito, estos 2 valores serian 0.
Saludos