Mediciones. El trazado de obras de gran extensión demanda, necesariamente, la intervención de topógrafos y el empleo de instrumentos y equipos apropiados; sin embargo, el trazado de obras de reducida a mediana extensión es posible realizarlo simplemente con huincha y cordeles, siempre y cuando se lleve a cabo con apropiado esmero a efecto de conseguir la exactitud deseada.
De preferencia la huincha será metálica, de longitud no menor de 25 m. Es necesario indicar a los ayudantes cuál es el cero de la huincha, pues, como sabemos , las huinchas están provistas de argollas que, en algunos tipos de huincha, no forman parte de la longitud real de las mismas. También es indispensable que la huincha, al efectuar las mediciones, sea fuertemente tensada.
Las mediciones deben ser horizontales, pues como tales están indicadas en los planos. Cuando las medidas son tomadas apoyando la huincha en terrenos de moderada pendiente el error en que pueda incurrirse no tiene mayor significación. No sucede lo mismo cuando el terreno tiene pronunciada pendiente; en este caso, es preciso tomar medidas horizontales progresivamente por tramos, a este método se le denomina medición por cultelación.
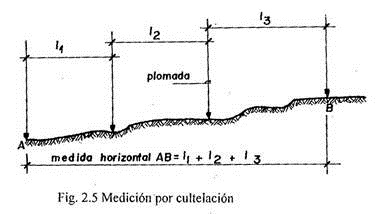
Por ejemplo, la longitud entre los puntos A y B es la suma de las medidas parciales I1, I2, I3 (Fig. 2.5).
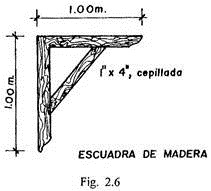
Empleo de escuadras. Las escuadras de madera, similares a la que muestra la Fig. 2.6, son, sin duda, útiles para trazos complementarios o de reducida longitud; no es recomendable su empleo para trazados de mayor extensión. Desde luego, debe desecharse, por no proporcionar la necesaria exactitud, la utilización de pequeñas escuadras de fierro.
Trazar una perpendicular a un alineamiento dado. Trazar una perpendicular a un alineamiento equivale a trazar un ángulo recto, es decir, de 90°.
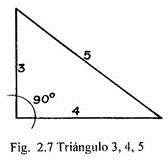
El procedimiento para trazar un ángulo de 90° se fundamenta en el principio siguiente: si los lados de un triángulo miden 3,4 y 5 m el ángulo formado por los lados que miden 3 y 4 m es un ángulo recto (Fig. 2-7).
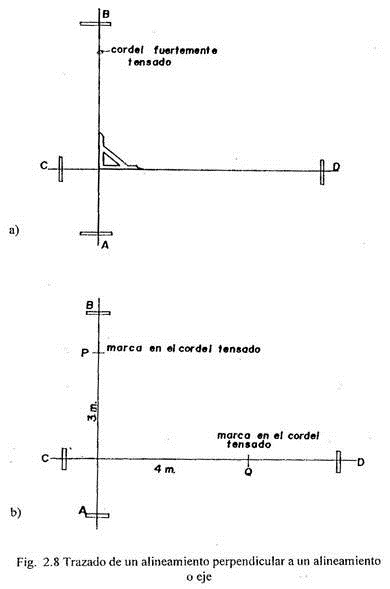
Ejemplo: Se trata de trazar un alineamiento perpendicular a un alineamiento o eje, AB (Fig. 2.8-a).
Procedimiento:
a) Tensamos un cordel entre las vallas A y B, definiendo así el alineamiento AB. Los travesaños de las vallas deben estar al mismo nivel.
b) Tensamos un cordel entre las vallas C y D auxiliándonos con una escuadra de madera. Aún no podemos asegurar que el alineamiento CD sea exactamente perpendicular al alineamiento AB.
c) A partir de la intersección de los dos cordeles medimos 3 m sobre el cordel AB, esta medida la marcamos en el cordel estableciendo el punto P. Una vez hecha la marca no se debe modificar la tensión del cordel AB (Fig. 2.8-b).
d) Exactamente hacemos lo mismo sobre el cordel CD pero tomando en este caso una medida de 4 m, definiendo el punto Q.
e) Verificamos con la huincha si la medida entre los puntos P y Q es 5 m. Si esto se cumple, los alineamientos AB y CD son perpendiculares entre sí. Es preciso que la comprobación se realice cuidadosamente.
f) De no cumplirse la condición indicada corregir el alineamiento CD, repitiendo el procedimiento tantas veces cuantas sean necesarias hasta conseguir el triángulo 3,4,5. Es indispensable, en cada corrección, tomar nuevamente las medidas 3 y 4 m sobre los cordeles AB y CD respectivamente, no siendo válidas las marcas anteriores
Trazar una paralela a un alineamiento dado, separada una distancia “d” de dicho alineamiento (Fig. 2.9).
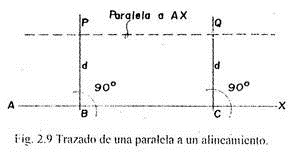
Procedimiento:
a) Desde los puntos B y C, convencionalmente escogidos sobre el alineamiento AX, trazamos perpendiculares a AX.
Si la distancia d es reducida se puede emplear una escuadra de madera para trazar las perpendiculares. Si la distancia es grande procede aplicar el método descrito en 2.2.3.
b) En las perpendiculares trazadas y a partir de los puntos B y C medimos la distancia prevista “d”, estableciendo los puntos P y Q.
c) Uniendo los puntos P y Q obtenemos la paralela buscada.
2.1.5. Dados un alineamiento base y un punto por el que debe pasar una paralela a dicho alineamiento, trazar la paralela. En la Fig. 2.10-a, AX es un alineamiento base y B es un punto por el que debe pasar una paralela a AX.
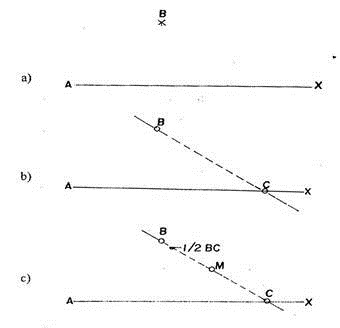
Procedimiento:
a) Ubicamos en el alineamiento AX un punto cualquiera, tal como C. Tendemos un cordel que una los puntos B y C (Fig. 2.10 b).
b) Dividimos por mitad el segmento de recta BC determinando el punto M (Fig. 2.10-c).
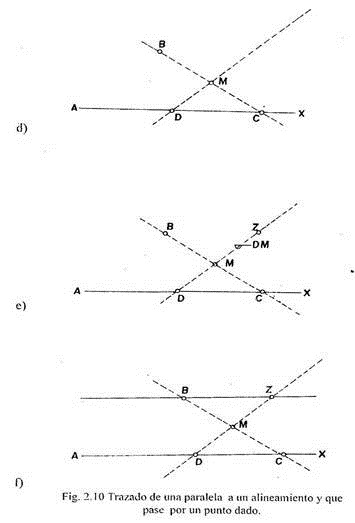
c) Desde un punto D, elegido arbitrariamente sobre AX, establecemos mediante cordel el alineamiento DM (Fig. 2.10-d).
d) Sobre el alineamiento DM y a partir el punto M medimos una distancia igual a DM, obteniendo así el punto Z (Fig. 2.10-e).
e) Uniendo los puntos B y Z trazamos la paralela buscada (Fig. 2.10-f).
Trazado de ángulos. El trazado de alineamientos que forman determinados ángulos con un alineamiento dado es posible realizarlo empleando el método de la tangente trigonométrica.
El procedimiento consiste en tomar sobre el alineamiento dado, digamos AX, a partir del vértice previsto una distancia convencionalmente escogida, estableciendo, de esta manera, el punto C. Al segmento de recta AC lo designamos base (Fig. 2-11).
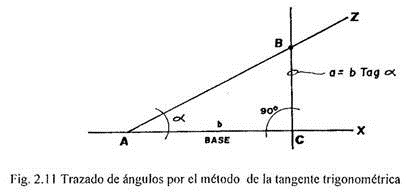
Desde el punto C trazamos una perpendicular al alineamiento AX. Sobre esta perpendicular y a partir del punto C tomamos una longitud igual al producto de la longitud de la base, AC, por la tangente del ángulo propuesto, definiendo así el punto B.
Uniendo los puntos A y B y prolongando la recta obtenemos el alineamiento AZ que forma con el alineamiento AX el ángulo previsto.
Es recomendable que la longitud de la base sea de 2, 3, 4, 5 m. Cuanto más grande es la base, mayor será la exactitud que cabe esperarse; aunque es pertinente advertir que cuando se trata de ángulos grandes l longitud de la perpendicular resulta excesiva e inconveniente para el trazado.
Aun cuando la tabla 1. está referida sólo a algunos ángulos es de utilidad práctica. Para ángulos que no figuran en la Tabla, las tangentes pueden obtenerse de computadoras provistas de funciones trigonométricas.
Desde luego, el grado de exactitud que se logre con el método descrito depende del esmero con que se realice. Su empleo es aceptable en obras relativamente pequeñas, mas no en proyectos que demanden mayor precisión, en los que, generalmente, se recurre a topógrafos y equipos de ingeniería.
Tabla 1. Valores de “a” (m) para trazar ángulo (Ver Figura 2.11).
| Ángulos | Base (m) 2 | 3 | 4 | 5 | |
| 10°15°
20° 25° 30° 35° 40° 45° 50° 55° 60° 65° 70° |
0.350.54
0.73 0.93 1.15 1.40 1.68 2.00 2.38 2.86 3.46 4.29 5.49 |
0.530.80
1.09 1.40 1.73 2.10 2.52 3.00 3.58 4.28 5.20 6.43 8.24 |
0.711.07
1.46 1.87 2.31 2.80 3.36 4.00 4.77 5.71 6.93 8.58 10.99 |
0.881.34
1.82 2.33 2.89 3.50 4.20 5.00 5.96 7.14 8.66 10.72 13.74 |
|
Ejemplo: Trazar un alineamiento AZ que forme un ángulo de 20° con un alineamiento dado AX (Fig. 2.12).
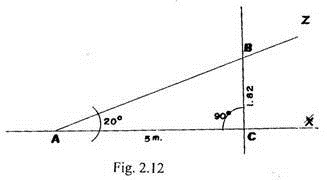
a) Sobre el alineamiento AX y a partir del punto A tomamos una longitud de 5 m, estableciendo el punto C.
b) Desde el punto C trazamos una perpendicular a AX.
Medimos en esta perpendicular a partir del punto C una longitud igual al producto de 5 m por la tangente de 20°, determinando el punto B.
Como la tangente de 20° es 0.36397, la longitud a tomarse será 5 x 0.36397 = 1.82 m, coincidente con el valor que figura en la tabla 2.1 para un ángulo de 20° y una base de 5 m.
c) Uniendo lo puntos A y B y prolongando la recta se obtiene el alineamiento AZ, que forma un ángulo de 20° con el alineamiento AX.
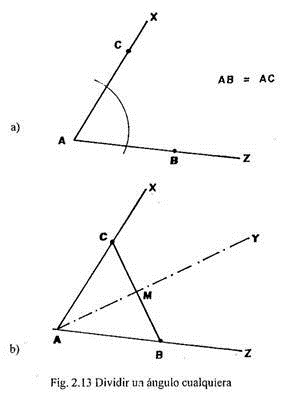
2.1.7. Dividir un ángulo cualquiera. Se trata de dividir por la mitad el ángulo formado por los alineamientos AX y AZ (Fig. 2.13).
Procedimiento:
a. En los alineamiento AX y AZ y a partir del vértice A tomamos una misma longitud definiendo los puntos B y C (Fig. 2.13-a).
b. Tendemos un cordel que una los puntos B y C.
c. Dividimos n mitad el segmento de recta BC, marcando en el cordel el punto M.
d. Uniendo el vértice A con el punto M y prolongando la recta se obtiene el alineamiento AY, que divide en la mitad el ángulo XAZ (Fig. 2.13-b).
Gracias a:


