Algoritmos genéticos
Ya habíamos visto una breve introducción de la computación evolutiva y ahora nos vamos a enfocar a los algoritmos genéticos. En la imagen vemos una aplicación en donde se utilizan para modelar el crecimiento de plantas.
Planteamiento del problema
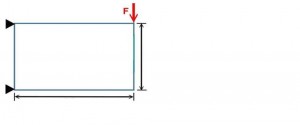
El problema de la Viga de Michell trata de buscar la configuración estructural que soporte la carga, que cumpla con restricciones de esfuerzos, desplazamientos y estabilidad; además debe ser la solución más económica posible.
Esto visto de forma matemática se expresa de la siguiente manera:
Función objetivo: minimizar f(x)= min(Li,Ai,p,k)
Sujeto a: gi(x) < ri
g1(x)< d
g2(x)< esf
g3(x)< esb
g4(x)< k
Li: es longitud del elemento, Ai: área de la sección transversal del elemento, p: pensidad del material, k:constructibilidad, gi(x): función de restricción, d: desplazamiento permisible, esf: esfuerzo permisible, esb: esbeltez permisible,
Se vuelve un problema complejo debido a que la función objetivo está en contraposición de las restricciones. Además la constructibilidad es un factor subjetivo.
Operaciones básicas
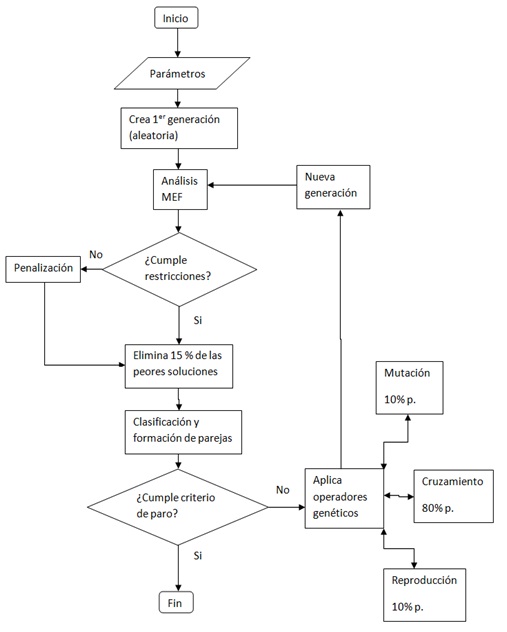
Un diagrama de flujo de un algoritmo genético se puede ver como el siguiente:
Al definir los parámetros uno debe ser cuidadoso con la representación que se vaya usar, debido a que esta guía la búsqueda. La representación generalmente es un vector binario pero también pueden ser matrices con números reales. Otros parámetros críticos son la cantidad de individuos por generación y el número de generaciones que nos estarían limitando la capacidad de búsqueda del algoritmo.
Dentro de las operaciones genéticas principales tenemos:
Mutación: Se hace un pequeño cambio en la representación y por lo tanto la solución es otra, ligeramente.
Apareamiento: Se forman parejas para después ser cruzadas.
Cruzamiento: Las parejas intercambian genes y forman la descendencia.
Reproducción: un individuo se copia a la siguiente generación sin cambios.
Secuencias de solución en la viga de Michell
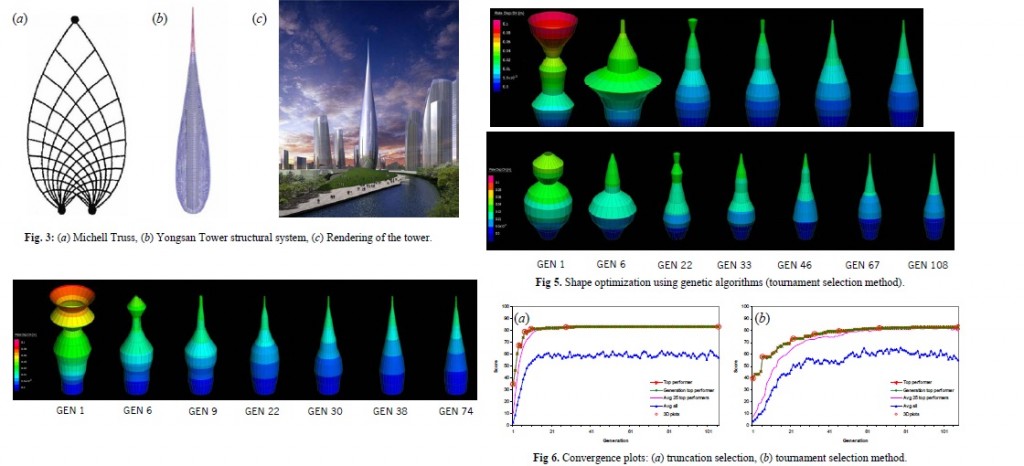
Ya preparado el algoritmo este se alimenta con propuestas aleatorias de solución y estas van evolucionando hasta que se alcanza el criterio de paro.
Las soluciones y aplicaciones prácticas
A continuación se presenta una aplicación practica de la viga de Michell.
¿Que otras aplicaciones le darías a la viga de Michell?….




Comments (1)
Yuri Villavicencio-Fdez - 27 octubre, 2011
Esto me recuerda más bien a los fractales. Me imagino que esta familiarizado con la Teoría de Juegos, supongo que en algo tiene que ver los aspectos de colaboración vrs. competencia en estos algorítmos, pero fui incapaz de visualizarlo. No me quedó nada clara la definición de las variables, le recomiendo que para futuras entregas dosifique la información. Recuerde que aquí, la mayoría de la Audiencia son alumno de pregrado y la verdad estos temas me parecen muy interesantes,pero hay que escribirlos de manera más asequible al público general.