Los polígonos de Thiessen nombrados en honor al meteorólogo estadounidense Alfred H. Thiessen son una construcción geométrica que permite construir una partición del plano euclídeo. Estos objetos también fueron estudiados por el matemático Georgy Voronoi de donde toma el nombre alternativo de diagramas de Voronoi y por el matemático Gustav Lejeune Dirichlet de donde toma el nombre de teselación de Dirichlet.
Los polígonos de Thiessen son uno de los métodos de interpolaciónmás simples, basado en la distancia euclidiana, siendo especialmente apropiada cuando los datos son cualitativos. Se crean al unir los puntos entre sí, trazando las mediatrices de los segmentos de unión. Las intersecciones de estas mediatrices determinan una serie de polígonos en un espacio bidimensional alrededor de un conjunto de puntos de control, de manera que el perímetro de los polígonos generados sea equidistante a los puntos vecinos y designando su área de influencia.
Si hay dudas, se resuelven comparando las distancias a los pluviómetros.
Una vez calculados, los coeficientes de Thiessen (ai / A) no cambian, por lo que es fácil usar el método para muchos eventos o períodos distintos. Si en algún caso faltaran datos en una estación, es más fácil estimarlos que rehacer todos los polígonos obviando tal pluviómetro. Si se altera la red hidrometeorológica, sí deben recalcularse los coeficientes del método.
Esta metodología es objetiva y entrega resultados satisfactorios si se tiene una red adecuada de pluviómetros. No es recomendable en áreas montañosas, ya que los coeficientes no reflejan de ninguna manera los efectos altitudinales, y tampoco se recomienda su aplicación para derivar promedios regionales en el caso de tormentas locales intensas.
Inicialmente los polígonos de Thiessen fueron creados para el análisis de datos meteorológicos (estaciones pluviométricas) aunque en la actualidad también se aplica en estudios en los que hay que determinar áreas de influencia (centros hospitalarios, estaciones de bomberos, bocas de metro, centros comerciales, etc.). Es una de las funciones de análisis básicas en los SIG.
Para la aplicación de los polígonos de Thiessen se requiere el conocimiento de la ubicación de cada estación dentro o en la periferia de la cuenca para proceder a su aplicación, identificando el área de influencia de cada pluviómetro y/o pluviógrafo. Así se van formando triángulos entre las estaciones más cercanas uniéndolas con segmentos rectos sin que éstos se corten entre sí y tratando que los triángulos sean lo más equiláteros posibles.
A partir de allí se trazan líneas bisectoras perpendiculares a todos los lados de los triángulos, las que al unirse en un punto común dentro de cada triángulo conforma una serie de polígonos que Facultad de Ingeniería Departamento de Hidráulica delimitan el área de influencia de cada estación. El área de influencia de cada estación considerada “Polígono” está comprendida exclusivamente dentro de la cuenca.
La precipitación media es:
Donde:
P = precipitación media sobre la cuenca
Pi= precipitación observada en la Estación i
Ai= área del polígono correspondiente a la Estación i
A= área total de la cuenca
n= número de estaciones pluviométricas y/o pluviográficas con influencia en la cuenca
El cálculo ordenado de la lluvia media por el método de Thiessen se realiza utilizando la siguiente Tabla:


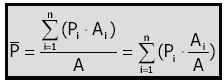
Comments (4)
Yuri Villavicencio-Fdez - 24 septiembre, 2011
Esta fue una de mis clases favoritas en la U, y una de las que más trabajé.
Yuri Villavicencio-Fdez - 24 septiembre, 2011
Importante: ArcGis 9.x en adelante ya realizan los cálculos de Polígono de Thiessen de manera automática-
adeluna100 - 25 septiembre, 2011
Mil gracias por el aporte.
Humberto H - 6 junio, 2013
Muchas gracias, se podría mejorar la calidad del articulo con imágenes del calculo y un ejemplo.