….Si observamos la matriz veremos que es simétrica y que en su diagonal nunca hay ceros porque esta son las solicitaciones que colocamos para provocar los desplazamientos unitarios. Los valores restantes son las reacciones a estas solicitaciones. Estas afirmaciones siempre se cumpliran en una matriz de rigidez.
Cuando planteemos las ecuaciones matriciales de [K].{x} = {F} las incógnitas a buscar serán las reacciones en los nudos restringidos y los desplazamientos en los libres. Los desplazamientos que si conocemos son donde hay apoyos (x=0). Las fuerzas conocidas son las cargas aplicadas.
Si colocamos una fuerza hacia la izquierda de 100 lb en el nudo 2 y sabiendo que los apoyos y 4 no tienen desplazamientos por lo cual no son incógnitas sino que son datos conocidos en los x=0. De igual manera aparte de la carga en el nudo 2 no existe otra, pero si tenemos incógnitas en los apoyos 3 y 4:
Fíjense que la carga en dos de 100 tiene signo negativo porque esta dirigida hacia la izquierda.
Una forma rápida de despejar las incógnitas es subdiviendo las matrices y ahora se notara la ventaja de haber numerado los nudos de la manera en que se hizo:
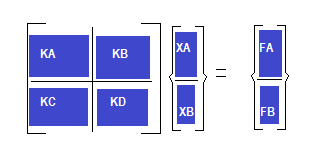
Cada division es una submatriz:
Ahora podemos plantear las ecuaciones separadas:
[KA].{XA}+[KB].{XB} = {FA}
[KC].{XA}+[KD].{XB} = {FB}
Como {XB} solo tiene ceros se simplifica el trabajo:
{XA}= {FA} = ;x1=-0.667; x2=-1.333
Sustituyendo en la segunda ecuación los valores hallados de x1 y x2 hallaremos {FB}= ; F3=33.33; F4=66.67
En el proximo articulo pasaremos a analizar casos aplicados como en armaduras.


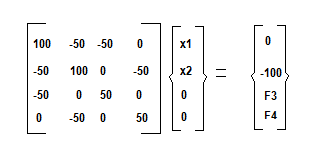
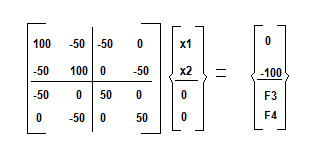
Comments (5)
Metuq - 24 febrero, 2012
suelta toda la información de una vez, previamente saludos y agradecimiento por el aporte. Gracias
Ing. José Cabrera - 24 febrero, 2012
Gracias por el comentario. El concepto que tenemos es brindar literatura breve, concisa y comprensible ya que si fuese muy larga la tendencia es que las personas tienden a obviar los articulos largos.
José L. Sandoval - 27 febrero, 2012
Gracias ing. Cabrera, estaba revisando precisamente estos temas.
Hector - 26 marzo, 2012
Gracias Ing. Cabrera, espero el próximo artículo
sandro casas - 13 abril, 2014
un buen libro para el método de rigidez