El Acertijo Civilgeeks de la semana me llegó vía el Facebook de mi amigo Luis, desde San Francisco en California. Me pareció tan sencillo y elegante que pensé en compartirlo esta semana. Dada la siguiente ecuación y su supuesto (i es igual a raíz cuadrada de -1) ,
Se les pide:
a) Determinar el resultado de la ecuación,
b) Justificar su resultado explicando el procedimiento.


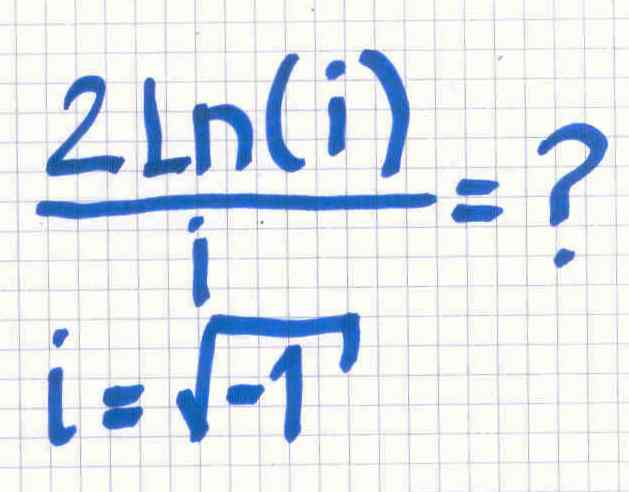
Comments (37)
Franco- Estudiante de Ing. Civil - 31 octubre, 2011
Puede que sea 2i ? yo lo asemejo a la relacion Sen(x)/x el cual tiene por resultado ‘x’… no se la verdad… es lo primero que se me ocurre…
Yuri Villavicencio-Fdez - 31 octubre, 2011
No…
Anthony Polanco - 31 octubre, 2011
La solución es Ln(1), es decir 0.
-Subo la i del denominador como i elevada a la -1 y la eq. queda 2*i^(-1)* ln(i).
-Luego meto la i^-1 adentro del logaritmo para que sea el exponencial de la i de dentro del ln.
-Cambio todas las «i» por raiz de -1. dentro del logaritmo me queda (raiz de -1)^((raiz de -1)^1).
-como estoy elvando (raiz de -1) a 2 exponentes puedo multiplicar los exponentes es decir -1 y (raiz de -1) –> de esa multiplicacion puedo obtener -1^(3/2) lo cual es igual a -1.
Entonces hasta ahora tendria 2 ln( (raiz de -1)^-1).
Raiz de -1 ^ -1 = 1/ raiz de -1… si racionalizamos esto tenemos -1*(raiz de -1) lo cual desde arriba sabemos que es igual a -1 ^(3/2) y que es igual a -1.
nos queda 2 Ln (-1), pasamos el 2 a ser el exponente del -1 y nos quedamos con Ln -1^2 = (((((Ln 1))))) <— Respuesta
Yuri Villavicencio-Fdez - 31 octubre, 2011
nop, acordate que b*ln a= ln a^(b) , desde el segundo paso está mal.
pablo segura - 31 octubre, 2011
mmmm y si el logaritmo lo eliminamos con una (e) nos qedaria 2i/i y ps creo qe ahi se eliminaria la i 😀 y el resulatado seria 2 … no estoy seguro haber si le atine 😛
Yuri Villavicencio-Fdez - 31 octubre, 2011
nop 😛 😀
Misaelo Salazar - 31 octubre, 2011
1) Ln i = i*pi/2….(*)
2) REEMPLAZANDO
3) (2*ln(i))/(i)=(2*(i*pi/2))/(i)
=despejando keda «pi»..
ojala este bn…
saludos.
CivilGeek - 31 octubre, 2011
Del gran Euler tenemos e^(Π*i)+1=0
Acomodando a nuestra conveniencia (i^2=-1)
e^(Π*i)=-1=i^2
Tomamos logaritmo natural
Π*i=2*ln(i)
Ordenando
Π=2*ln(i)/i
Y la respuesta sería Π = 3,1416
Vinicio - 1 noviembre, 2011
efectivamente la respuesta es π,y mi Calculadora Voyage 200 también dice lo mismo.
David - 25 noviembre, 2011
La respuesta de CivilGeek parece correcta, pero no tiene sentido porque el logaritmo neperiano sólo está definido para números reales, es decir, ln(i) simplemente no existe.
Es como la siguiente aparente contradicción:
Supongamos que a = b
Multiplicando por a: a^2 = a·b
Restando b2: a^2 – b^2 = a·b – b^2
Factorizando a la izquierda: (a + b) · (a – b) = a·b – b^2
Factorizando a la derecha: (a + b) · (a – b) = b · (a – b)
Simplificando: a + b = b
Como a = b, sustituyendo: b + b = b
Por tanto: 2·b = b
Simplificando: 2 = 1
Obviamente hay un error, ¿pero dónde?
Luis M Ferrero - 22 diciembre, 2011
Respondiendo a David, no puedes simplificar (a-b) porque si a=b entonces a-b=0 y no podemos simplificar de esa forma. Lo que escribes es lo mismo que pensar que si 2*0=3*0 entonces 2=3. El cero es elemento singular del producto y, claro, no tiene elemento simétrico respecto de esa operación. Hay que leer las propiedades del cuerpo de los reales.
Respecto de lo que dices de los logaritmos:
El logaritmo natural de un número complejo z es otro número complejo b = ln(z) que sea solución de la ecuación:
z = e^b
La ecuación anterior no tiene solución única. De hecho, tiene un número infinito de soluciones, aunque todas ellas son fáciles de encontrar.
An - 31 octubre, 2011
la respuesta es 2pi gracias a la bendita Hp
BRUNO CASTILLO EDUARDO ADOLFO - 1 noviembre, 2011
LA TENGO ES ASI:
e^(pi)*i+1=0 FORMULA DE EULER.
e^(pi)*i=-1
e^(pi)*i=i^2 Tomando logaritmo natural a ambos miembros.
(pi)*i = 2ln(i)
DONE FINALMENTE:
PI = 2LN(i)/i La saque rapidamente. =)
Buen reto ing. Yuri, GENIALLL
BRUNO CASTILLO EDUARDO ADOLFO - 1 noviembre, 2011
PERO ERA QUE NO DE EL DATO DE RAIZ DE MENOS UNO ES IGUAL A i. DESDE AHI LO DEJO MUY CLARO.
Carlos R Benitez - 4 noviembre, 2011
igual: π
carloder.1 UNI - 8 noviembre, 2011
el 2 lo paso como exponente d i, el i q divide lo multiplico por x (lo q quiero), lo llevo como exponente d e alos dos lados d la igualdad y por eluler sale cos(x)=i^2=-1
osea todos los (2k-1)π donde k pertenece alos naturales
Luis M. Ferrero - 19 diciembre, 2011
Disiento de todo lo expuesto, parece que no os contaron que en variable compleja un logaritmo siempre tiene infinitas soluciones. Aplicando la relación de Euler:
i=e^(i(π/2 + 2kπ))
aplicando logaritmos
Lni=i(π/2 + 2kπ)
dividiendo por i y multiplicando por 2
2/i*Lni=π + 4kπ
es decir que las respuestaSSSSS que son muchas son
(4k + 1)π para todo k perteneciente a los enteros
jeje bueno, la solución expuesta anteriormente por la web es algo simple porque es una, no infinitas
Un saludo
Rick Ortiz - 4 septiembre, 2012
y al final Yuri Villavicencio-Fdez nunca dijo la respuesta… como para asegurarnos cual es la forma correcta de desarrollarlo
hugo rios - 6 septiembre, 2012
david si a=b entonces a-b=0 por lo que no se puede hacer la división al simplificar ya que no esta definida la division por cero
Alexander - 29 octubre, 2012
2*Ln(i)/i=x (multiplicando por i y elevando por el numero e )
e^(Ln(i)^2)=e^(x*i) (simplificando ya que e es el inverso de Ln)
(i)^2=e^(x*i) (pero i=(-1)^0.5)
-1=e^(x*i) (re-ordenando se tiene)
e^(x*i)+1=0 y como ya sabemos es la ecuación de Euler, conocida como la Fórmula mas bella.
e^(x*i)+1=0 => e^(π*i)+1=0, por lo tanto X=π.
Buen acertijo.
Saludos.
Carlos Martinez - 12 enero, 2013
Una respuesta: pi.
Procedimiento:
2 Ln(i) / i
——– = x / * —
i / 2
Ln(i) = i * x / 2 / exp[]
i = e^(i*(x/2)) (*)
Por Identidad de Euler:
e^(i*x) = cos(x) + i*sen(x) (**)
Aplicando (**) en (*):
i = cos(x/2) + i * sen(x/2)
Se comprueba que solo hay un valor posible: pi.
Luis Arturo - 7 abril, 2013
Hola que tal tengo entendido que si se tiene una raíz cuadrada con signo negativo se obtiene un numero imaginario pero en esto caso la ecuación es indeterminada por la misma razón y en todo caso de que la raíz fuera positiva el resultado es 0, ya que ln(1) = 0 y 0/1 = 0.
Ing. Jose R. Cabrera - 8 abril, 2013
Yuri, te lo he dicho antes, creo que es una falta de respeto al publico
dejar abierta una pregunta y mas si tiene mas de 1 dia. Esta, tiene varios anos…..
Filiberto Toledo - 7 octubre, 2013
Si ln 1 = 0 y e^0= 1
ln i =x e^x = i
Por lo tanto (2e^x)/i = i Si elevamos los dos lados al cuadrado Se obtiene:
(4e^2x)/-1 = -1 ===> e^2x= 1/4
Entonces: ln(1/4)= 2x
X= -0.69314718
Será???
Saludos!!!
Vilomar Sanchez - 17 enero, 2014
la respuesta es Pi
Vilomar Sanchez - 17 enero, 2014
la respuesta es Pi.
jhon - 18 enero, 2014
La respuesta es pi()
Tenemos:
A×LN(b)= LN(b)^A
LN(-1)=i×pi()
i=(-1)^(1/2)
2×LN(i)/i= LN((-1)^(1/2))^2/(-1)^(1/2)
LN(-1)/(-1)^(1/2)=i×pi()/-1^(1/2)
(-1)^(1/2)×pi()/-1 ^(1/2)= pi.
eloy garabito - 26 mayo, 2014
felicitaciones por preucuparse de los estudiantes de ingenieria civil gracias con sus aportes en bibliofias y experiencias de ustedes
climaco - 27 junio, 2014
A ver q tal este desarrollo h q pertenezca a los Reales
haciendo h=(2ln(i))/i Despejando i=e^((i*h)/2) por Euler i=sin〖h/2+i*cos〖h/2〗 〗
Despejando i queda i=cos〖h/2〗/(1-sin〖h/2〗 ) elevando al cuadrado ambos miembros
i^2=(cos〖h/2〗/(1-sin〖h/2〗 ))^2 Entonces (cos〖h/2〗/(1-sin〖h/2〗 ))^2=-1 (cos〖h/2〗 )^2=-(1-sin〖h/2〗 )^2
{(cos〖h/2〗 )^2+ (sin〖h/2〗 )^2 }+1=-2*sin〖h/2〗 por propiedad {(cos〖h/2〗 )^2+ (sin〖h/2〗 )^2 }=1
Entonces despejando queda sin〖h/2〗=1 por tanto
h=2*sin^(1)
Por tanto (2ln(i))/i∈{2*sin^(1) }≈π
climaco - 27 junio, 2014
A ver q tal este desarrollo h q pertenezca a los Reales
haciendo h=(2ln(i))/i
Despejando i=e^((i*h)/2)
por Euler i=sin〖h/2〗+i*cos〖h/2〗
Despejando i queda
i=cos〖h/2〗/(1-sin〖h/2〗 )
elevando al cuadrado ambos miembros
i^2=(cos〖h/2〗/(1-sin〖h/2〗 ))^2
Entonces (cos〖h/2〗/(1-sin〖h/2〗 ))^2=-1 (cos〖h/2〗 )^2=-(1-sin〖h/2〗 )^2
{(cos〖h/2〗 )^2+ (sin〖h/2〗 )^2 }+1=-2*sin〖h/2〗 por propiedad {(cos〖h/2〗 )^2+ (sin〖h/2〗 )^2 }=1
Entonces despejando queda sin〖h/2〗=1 por tanto
h=2*sin^(1)
Por tanto (2ln(i))/i∈{2*sin^(1) }≈π
CHARLES HERNAN - 14 noviembre, 2014
La respuesta es «pi»
Utilizo la forma de Euler.Z=re^øi.
Lni=LnZ, Z=i=0+i, entonces: r=(0^0.5 + 1^0.5)^0.5 ..r=1…. y tang(ø)=1/0….entonces: ø=pi/2
luego: Z=1e^(pi/2)i =e^(pi/2)i…aplicando logaritmo neperiano: LnZ=Ln(e^(pi/2)i)=(pi/2)i.
Remplazando en la proposicion: (2Lni)/i: [(2[(pi/2)i])/i]=pi…por lo tanto la rpta. es: ¡¡¡¡ «pi» !!!!!
Johnner Alexander - 27 noviembre, 2014
Hola
Si es facil
la respuesta es 0
por que
(2Ln (-1)^(1/2))/i = (Ln(-1)^2)/(2*i)
luego queda simplemente
(Ln(1))/(2i) = 0/(2i) = 0
ariel choque - 7 abril, 2015
Segun analisis de variable compleja. Resp. ln(-1) = Ln(1) +i((pi)+2(pi)k) , luego las i se simplifican y queda (pi) + 2(pi)k donde k pertenece a los enteros
rolando lopez nuñez - 21 junio, 2015
2ln(i)/i=? e^2ln(i)/e^i e^ln(i^2)/e^i i^2/e^i -1/e^i (utilizando la identidad de euler e^(iπ)+1=0
se tiene que e^i=-1^(1/π) )… se sustituye en la ultima ecuacion y se tiene
-1/e^i -1/-1^(1/π) -1^(1-1/π) el resultado es -1
fue un placer en solucionar este acertijo espero los siguientes
rolando lopez nuñez - 21 junio, 2015
el resultado es -1
marco - 10 septiembre, 2015
es pi, por propiedades de logaritmo,
ln(i)=ln((-1)^(1/2))=(1/2)*ln(-1)
e^(i*pi)=-1
ln(-1)=i*pi
2*(1/2)*i*pi/i=pi
Martin - 14 julio, 2016
2*Ln(i)/i = x
Ln(i) = i*x/2
i=exp(i*x/2)
i=cos(x/2)+isin(x/2)
por tanto cos(x/2) = 0 y sin(x/2)=1 de donde x/2= Pi
esto es x=2*Pi