Hoy decidí publicar temprano. Nuevamente con un asunto de velocidad (de pensamiento). Hay que resolver la ecuación:
x=cos (x)
en menos de 15 segundos, utilizando métodos numéricos que no impliquen el uso de calculadoras gráficas, ni programas sofisticados de calculadora.
Obs.1 : La ecuación mostrada equivale a encontrar el Intersepto en x de la función f(x)= x-cos(x), que se muestra en el gráfico que sigue:
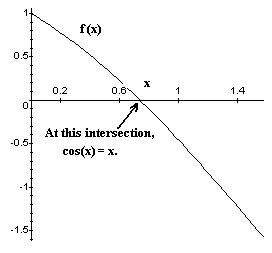
Una vez que pasen los 15 segundos, puede seguir leyendo para comprobar su respuesta.
Si usted obtuvo como resultado:
0,73908513321516064165531208767387…
o cualquiera de sus aproximaciones, está en lo correcto. Su puede utilizar el método numérico para la obtención de raíces de Newton. Pero seguramente le tomará más de diez minutos. Este número se puede obtener fácilmente pulsando repetidamente la función «coseno» de su calculadora. Lo interesante es que no importa el primer número que usted coloque en la entrada, a medida que usted continúe pulsando la función, el resultado se acercará invariablemente a este resultado. Esta propiedad ha hecho que este tipo de números se denominen «atractores» y son estudiados en matemáticas superiores en la construcción fractales.


Comments (1)
Martin - 14 julio, 2016
x=sin(x)
a segundo orden sin es:
sin(x) aprox igual 1+x^2/2
entonces tenemos que resolver
x=1+x^2/2
x^2+2*x -2 = 0 una ccucación de segundo grado.
La solución es de la forma
x=[-(2)+sqrt(4-4(1)(-2)]/2(2)
x=-1+sqrt(3)
x=0.7320508076