Disponemos de una columna lisa de radio r y de una cuerda delgada de longitud k. Con un nudo corredizo rodeamos la columa y en el extremo libre atamos un perro. En cierto momento el can ve acercarse a su amo y corre hacia él.¿A qué distancia de la columna queda el nudo cuando la cuerda se rompe?
Veamos las formas de solucionar desde ambos puntos de vista:
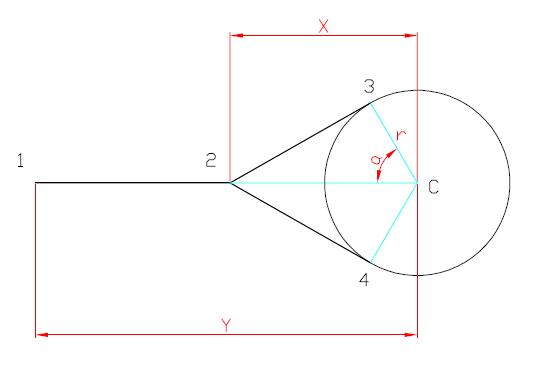
Desde un enfoque totalmente matemático deberíamos pensar que el perro se aleja de la columna y cuando está a su máxima distancia, tira un poco más y rompe la cuerda, lo que significa que debemos calcular una expresión genérica de la distancia del perro a la columna (distancia 1-c, a la que llamaremos «y») dependiente de otra variable, que en este caso va a ser la distancia del nudo al centro de la columna (distancia 2-c, a la que llamaremos «x»). Una vez calculada estudiaremos cuál es el valor de x para el que y es máximo.
Para ello vamos primero a medir en el gráfico el valor de «k», la longitud del hilo k=d(1,2)+d(2,3)+arco(3,4)+d(4,2). Sustituyendo queda:
Observando que cosa=r/x entonces a=arccos(r/x). Si sustituimos en la expresión y despejamos y, ya tenemos la distancia del perro en función de x.
Derivando e igualando a cero, despejamos el valor crítico de x para el que y tiene máximo (se comprueba que lo es sustituyendo en la segunda derivada, ya sabéis).
Conocido el valor de x, la distancia pedida es D=x-r, es decir:
Desde un punto de vista físico ¿Qué situación permite al perro romper la cuerda? Que el nudo se haya detenido en una posición de equilibrio. Esta es la conjetura más importante: la situación de equilibrio de fuerzas en el nudo es la que posibilita que el perro tire un poco más y rompa. Si el nudo se desplaza aún no pasaría nada. ¿Cuáles son las fuerzas que actuan sobre el nudo? Evidentemente una por cada porción de hilo que accede al nudo, es decir 3. Lo que sabemos de esas fuerzas es que por ser columna e hilo sin rozamientos, las tres tienen igual módulo, direcciones las de los hilos y sentidos «tirando» del nudo. ¿Cómo pueden estar en equilibrio tres fuerzas concurrentes de igual módulo? Trivial, en posición de simetría de orden 3, es decir formando un ángulo de 2π/3 cada una con las otras dos. Ello significa que el ángulo 324 es de 2π/3 y por tanto a=π/6, al ser el triángulo 23c rectángulo en 3. Sabiendo eso es sencillo deducir x=r/cos(π/6), que asombrosamente es la misma respuesta calculada antes 😉


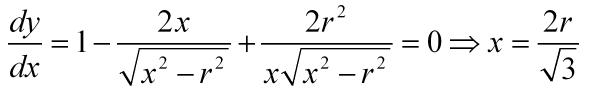
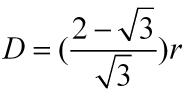
Comments (2)
CivilGeek - 8 febrero, 2012
Impresionante la solución desde el punto de vista físico.
La situación de equilibrio de fuerzas en el nudo es la que posibilita que el perro tire un poco más y rompa…
Excelente post!!!
Franz - 9 febrero, 2012
La fisica tendria que etar de mano con la matenatica, pero hay ratos que el razonamiento es mas sencillo que una expresion matematica, buena la pregunta y mejor la respuesta 🙂