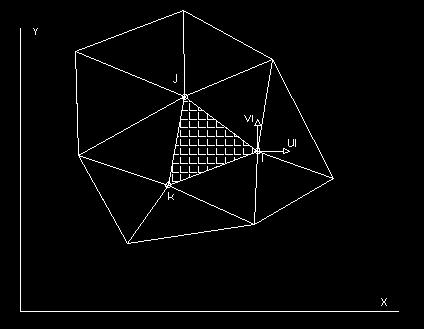
Para formular directamente las características de un elemento finito perteneciente a un problema continuo, vamos a estudiar un caso básico de tensión plana. Supongamos que dividimos la región a estudiar en elementos triangulares.
Mas sobre el Método de los Elementos Finitos ► https://civilgeeks.com/?p=13311
1.- Función de desplazamiento
El elemento finito típico como el cuadriculado en la figura, se define por sus nodos i, j, k y por los segmentos rectos que los unen. Debemos aproximar los desplazamientos de cualquier punto del elemento mediante un vector columna
En general las componentes de N son funciones de posición dadas y a es un vector formado por los desplazamientos nodales del elemento considerado. En nuestro caso:
Como función, u representa el movimiento horizontal y vertical de cualquier punto del elemento considerado.
Este último representa los correspondientes desplazamientos del nodo i. La idea consiste en conocer el desplazamiento de cualquier punto del triángulo, conocidos los desplazamientos de los vértices. En esencia esto puede hacerse mediante interpolación, y así se generan las funciones de forma N. Las características de estas funciones se describirán más adelante, pero es importante señalar que su elección es decisiva en el método de los elementos finitos.
2.- Deformaciones
Una vez conocidos los desplazamientos para todos los puntos del elemento, se pueden determinar las deformaciones mediante las ecuaciones clásicas de la elasticidad
Donde S es un operador matricial de la forma
y ε como vector generalizado de deformaciones unitarias es de la forma
Sustituyendo la ecuación (1) nos queda
Donde B es sencilla de conocer derivando convenientemente las funciones de forma.
3.- Tensiones
Procedentes de la ley de Hooke para el caso de tensión plana sabemos que, supuesto medio isótropo, considerando unas deformaciones iniciales debidas a cambios de temperatura, retracciones, cristalizaciones…y unas tensiones iniciales residuales (son los términos con subíndice cero):
Donde el tensor D es de la forma:
Y σ es el vector generalizado de tensiones, análogo en configuración al de deformaciones antes expresado
4.- Fuerzas nodales equivalentes
Son un conjunto de fuerzas y momentos aplicados en los nodos del elemento, estáticamente equivalentes a las fuerzas exteriores aplicadas sobre el citado elemento. Su determinación es sencilla y mecánica como veremos en el próximo capítulo.


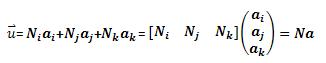
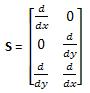
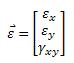
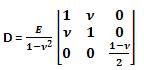
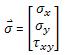
Comments (3)
ingeniev - 27 marzo, 2012
Felicitaciones por tratar este tema, es algo que muchos aun tenemos pendiente..
lokitosamax - 26 abril, 2012
El tema esta demasiado superficial la cual solo se esta estableciendo para elementos isotropicos es decir las principales ecuaciones de la Estática lineal en la cual se basa el PTV.
Esfuerzo=De
u=Na
deformacion unitaria=Ba y que deformacion unitaria=Su
de la cual la funcion B=SN
con la cual quedaria con el principio de trabajos virtuales y reduciendo valores quedaria de la siguiente manera:
K_{ij}=\int_{V}B^{T}DBdV
El primer informe de tesis habla de eso justo de los principios y de los cuales se puede iniciar el calculo de Vigas tanto en tensión como en flexion.
lokitosamax - 26 abril, 2012
pero no se como colgar el informe.