ESTRUCTURAS DE UN GRADO DE LIBERTAD: OSCILACIÓN ARMÓNICA, TEORÍA E HISTORIA.

Cuando analizamos en el análisis dinámico de una estructura de un grado de libertad (en el articulo anterior), su movimiento (le llamamos respuesta) en el tiempo, al final obtuvimos dos ecuaciones:

x=Acos(wt), o

                  x=Asin(wt)                        

Si tomamos cada una de estas ecuaciones y, en una hoja electrónica, a mano, con matlab o como quieran las resolvemos y graficamos obtendremos dos graficas parecidas. Supondremos que A=1.

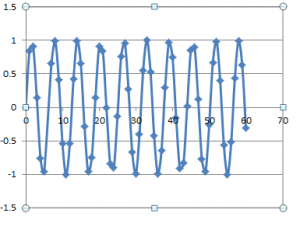
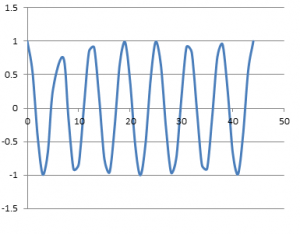
Fijense que la grafica superior empieza con la ordenada en O porque sin(O) = O  y la inferior se inicia en 1 porque cos(O) =1, dado que sus amplitudes iniciales, A=1.

Por la forma de las curvas, que van y vienen de igual forma, manteniendo la misma forma y parámetros en el tiempo se les conoce como oscilaciones armónicas, las cuales son ondas periodicas, se repiten a traves del tiempo. Todas las graficas de las ecuaciones como las anteriores explicadas a través de senos y cosenos son llamadas armónicas.

Si tomamos un resorte y logramos que baje y suba en el tiempo y, a la vez, ponemos un lápiz en el extremo del resorte y hacemos corre el papel horiontalmente, definirá la gráfica anterior que dibujamos con los resultados que, en mi caso hice con Excel. En la oscilación hay un equilibrio energético donde podemos sumar energía potencial y cinética y siempre se cumplirá el Principio de la Conservación de la Energía. El cuerpo, resorte, péndulo, cuerda, columpio, se mueve alrededor de su posición de equilibrio,. que es la linea recta inferior.  

Cada posicion refleja la suma de energia potencial y cinetica. Hay lugares, como los mas altos y bajos donde la energia potencial es toda la energia ya que al devolverse el resorte no hay movimiento, pero si maximos de posicion. Hay otros lugares, la posicion de equilibrio, donde la energia cinetica es maxima y la potencial es cero.

Quien primero planteo dicha situación fue Galileo. Estaba en misa, en la catedral de Pisa sentado atrás, distraído, observando como dos arañas se balanceaban en unas lámparas y le llamo la atención que el viento (Era Invierno) hacia oscilar algunas lámparas en un vaivén más largo que en otras.

“Claro, las que están más cerca de la puerta reciben el viento con más fuerza y se balancean más”, pensó Galileo. Pero no, estaba confundido porque percibía que aunque el vaivén fuera más o menos corto, todas las hacían en el mismo tiempo. “No debiera ser así ya que la más larga debería durar más tiempo en el vaivén”. Decidió probarlo, pero no estaba en el siglo XXI. El reloj que se disponía era un reloj de Sol en la Plaza del Ayuntamiento y no servía para medir tiempos pequeños. Tampoco se disponía de un reloj de arena, así que, como toda persona que no se deja amilanar se le ocurrió la mejor idea para la y época: Usar sus latidos del corazón para aproximar el tiempo.

Conto la primera: “6 latidos”. Otra vez: “8 latidos”,….”7 latidos”, nunca obtenía el mismo resultado. “Lo que hice es contar diez veces y dividir por 10”. Pudo comprobar que aunque las masas fueran diferentes el tiempo de oscilación (Periodo) era  el mismo (Probo con masas de madera y otras de oro). Había descubierto que Aristóteles estaba equivocado.

Luego probó con cuerdas colgantes de diferentes longitudes y ahí comprobó el dominio del tiempo: Las más larga obtenían mayores periodos de oscilación que las más cortas. Descubrió que el periodo de oscilación, T es proporcional a la raíz cuadrada de la longitud de la cuerda de la lámpara o péndulo. Con este descubrimiento se posibilito la fabricación de los engranajes del reloj mecánico.

En el primer artículo planteamos que w = Raíz(K/M) en el caso de la masa sujeta al resorte. En el péndulo w = Raiz(g/l) donde g es la aceleración de la gravedad y l el largo del péndulo. Si analizamos ambas fórmulas veremos que aunque se ven diferentes son similares ya que F = M.a que en este caso a = g  y M = F/g. Si lo introducimos en la fórmula de la masa con resorte:

w = Raíz (K/M) = Raíz (K.g/F) y como F = K.x,  w = Raíz (g/x) que es similar.

Esta frecuencia es llamada frecuencia circular, porque esta referida a un circulo. Para convertir a Periodos de tiempo o frecuencia, hay que tomar en cuenta que el circulo tiene 2.pi :

f = w/2.pi = (1/2.pi).Raiz(K/M)

 El periodo es el inverso de la frecuencia: T = 2.pi.Raiz(M/K)

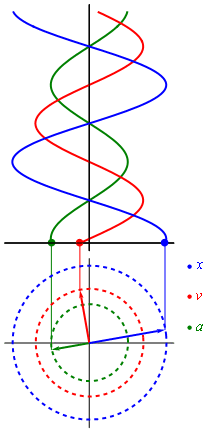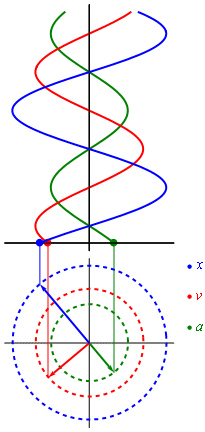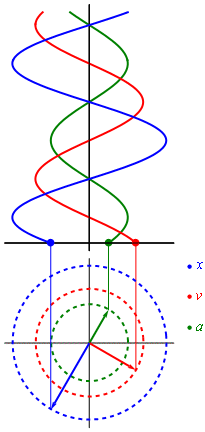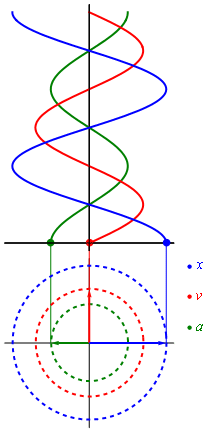
En la grafica final presentamos como se origina la respuesta x,v y a las cuales son ortogonales entre si. Fijense que la aceleracion se opone al desplazamiento ya que llevan direcciones contrarias.

Cosa curiosa: Galileo era amigo del Papa del momento, desde ante,s cuando era arzobispo, pero a pesar de ello fue condenado por

la Iglesia, que aunque no fue  finalmente condenado a muerte, tuvo que retractarse a peticion de sus amigos de la Iglesia y sufrir prision domiciliaria hasta su muerte. Esa prision le causo mucho sufrimiento. A pesar de ello murio de 78 anos.

Más adelante veremos como todo en la vida y el Universo puede ser explicado a través de las frecuencias y los periodos. Un caso es la música, otro es el cuerpo humano (Cada órgano tiene su frecuencia natural), los colores: El Universo es un fenómeno vibratorio.